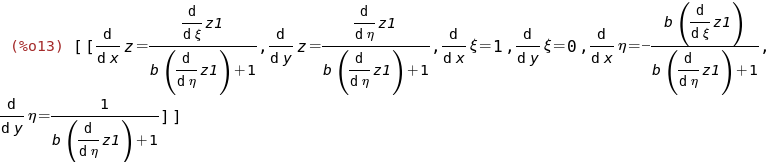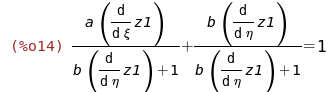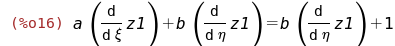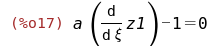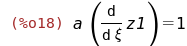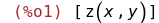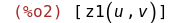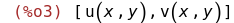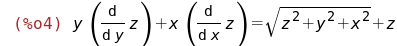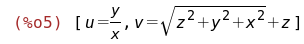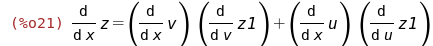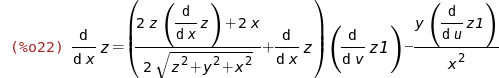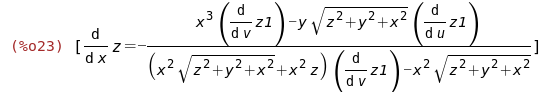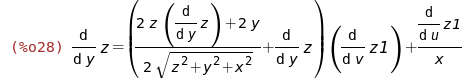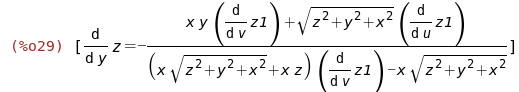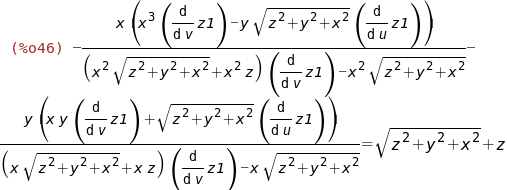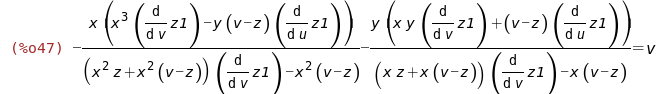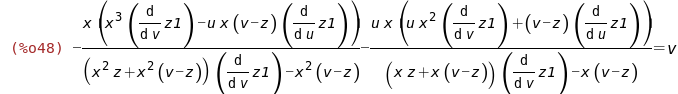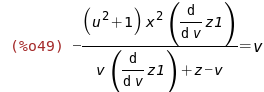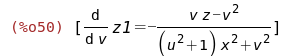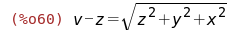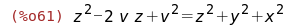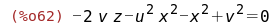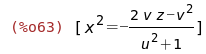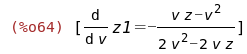Чтобы группе 606 не было так грустно делать д/з, выкладываю примеры скриптов, выполняющих эту работу в системе компьютерной алгебры Maxima для номеров 3460 и 3464.
3460:
В самом начале решения мы подразумеваем замену
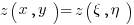
. Её мы делаем в уме и ничего по поводу неё не пишем, но компьютеру о ней нужно сказать явно. В частности, введя два разных
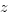
:
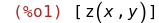
|
(%i2)
|
depends(z1,[xi,eta]);
|
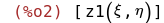
Новые переменные зависят от старых, о чём тоже нужно сказать:
|
(%i3)
|
depends([xi,eta],[x,y]);
|
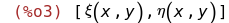
Самое важное. Уравнение, в котором нужно сделать замену:
|
(%i4)
|
eqn:a*diff(z,x)+b*diff(z,y)=1;
|
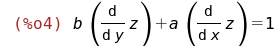
Функции перехода от старых переменных к новым:
|
(%i5)
|
zam:[xi=x,eta=y-b*z];
|
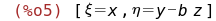
Вышеупомянутая замена
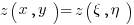
:
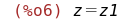
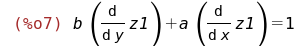
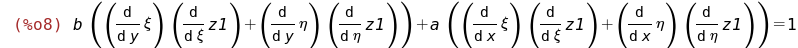
Во что превращаются
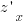
и
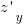
по формуле дифференцирования сложной функции многих переменных:
|
(%i9)
|
[diff(zz,x),diff(zz,y)];
|
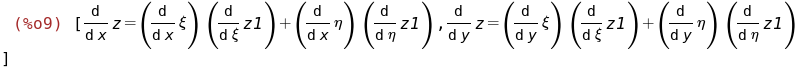
Чему равны производные новых переменных:
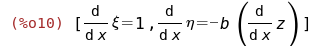
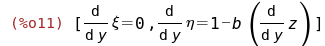
Теперь объединим три последних группы уравнений в систему:
|
(%i12)
|
append(%th(3),%th(2),%);
|
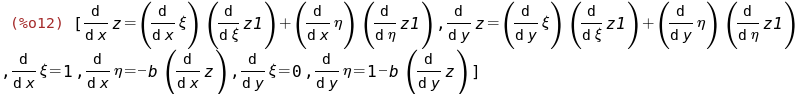
И решим её относительно производных
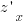
и
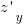
, избавив их от
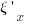
,
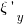
,
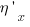
и
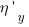
:
|
(%i13)
|
solve(%,[diff(z,x),diff(z,y),diff(xi,x),diff(xi,y),diff(eta,x),diff(eta,y)]);
|
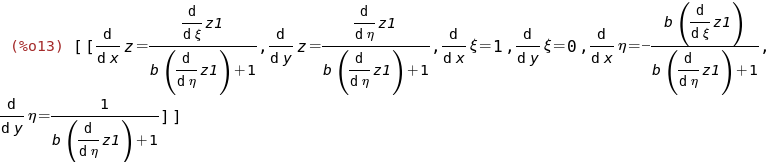
Подставим полученное в преобразуемое уравнение
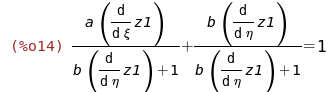
и упростим его:
|
(%i16)
|
radcan(eqn1*part(eqn1,1,1,2));
|
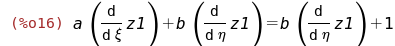
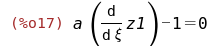
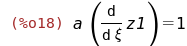
3464:
Осторожно, этот пример не является полной копипастой предыдущего, есть изменения:
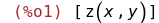
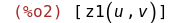
|
(%i3)
|
depends([u,v],[x,y]);
|
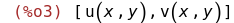
|
(%i4)
|
eqn:x*diff(z,x)+y*diff(z,y)=z+sqrt(x^2+y^2+z^2);
|
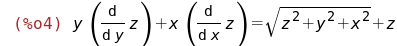
|
(%i5)
|
zam:[u=y/x,v=z+sqrt(x^2+y^2+z^2)];
|
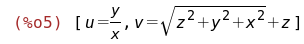
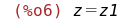
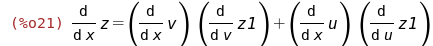
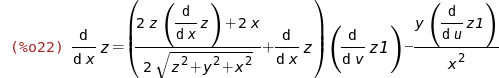
|
(%i23)
|
zx:solve(%,diff(z,x));
|
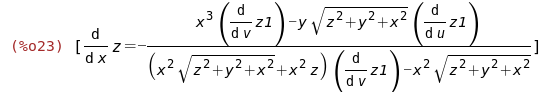
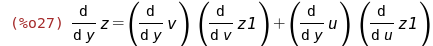
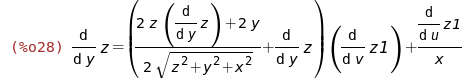
|
(%i29)
|
zy:solve(%,diff(z,y));
|
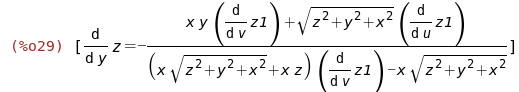
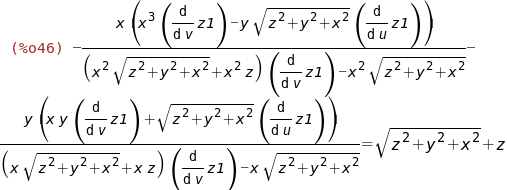
|
(%i47)
|
%,rhs(zam[2]-z)=lhs(zam[2]-z);
|
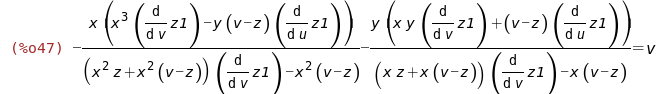
|
(%i48)
|
%,solve(zam[1],y);
|
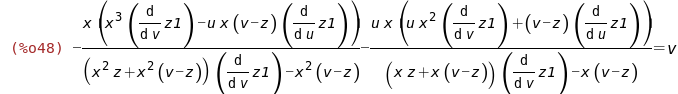
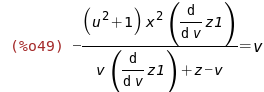
|
(%i50)
|
eqn1:solve(%,diff(z1,v));
|
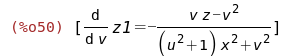
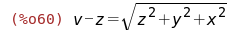
|
(%i62)
|
%-rhs(%),solve(zam[1],y);
|
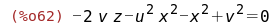
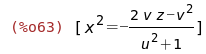
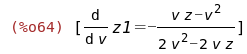
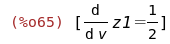
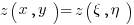 . Её мы делаем в уме и ничего по поводу неё не пишем, но компьютеру о ней нужно сказать явно. В частности, введя два разных
. Её мы делаем в уме и ничего по поводу неё не пишем, но компьютеру о ней нужно сказать явно. В частности, введя два разных 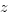 :
:
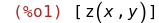
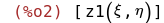
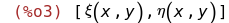
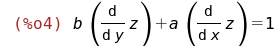
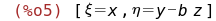
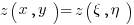 :
:
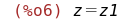
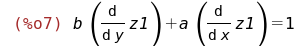
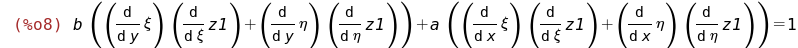
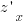 и
и 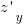 по формуле дифференцирования сложной функции многих переменных:
по формуле дифференцирования сложной функции многих переменных:
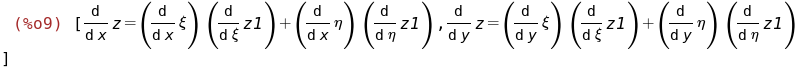
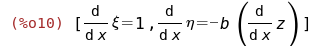
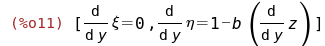
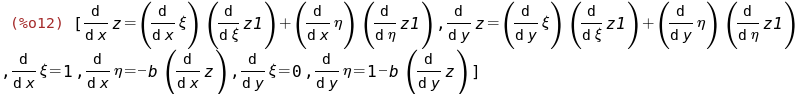
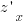 и
и 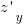 , избавив их от
, избавив их от 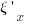 ,
, 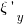 ,
, 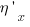 и
и 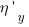 :
: