Объём тела равен интегралу от единицы по этому телу: \[ V=\iiint\limits_{V}1\cdot dxdydz \]
Демидович № 4103 Найти объём тела, ограниченного поверхностями \[ x^{2}+z^{2}=a^{2},\qquad x+y=\pm a,\qquad x-y=\pm a. \] Уравнение $x^{2}+z^{2}=a^{2}$ задаёт цилиндр радиуса $a$ вокруг оси $y$. Остальные уравнения задают плоскости, перпендикулярные плоскости $xy$. Вид на тело сверху, в плоскости $xy$, отображён на рис. 1:
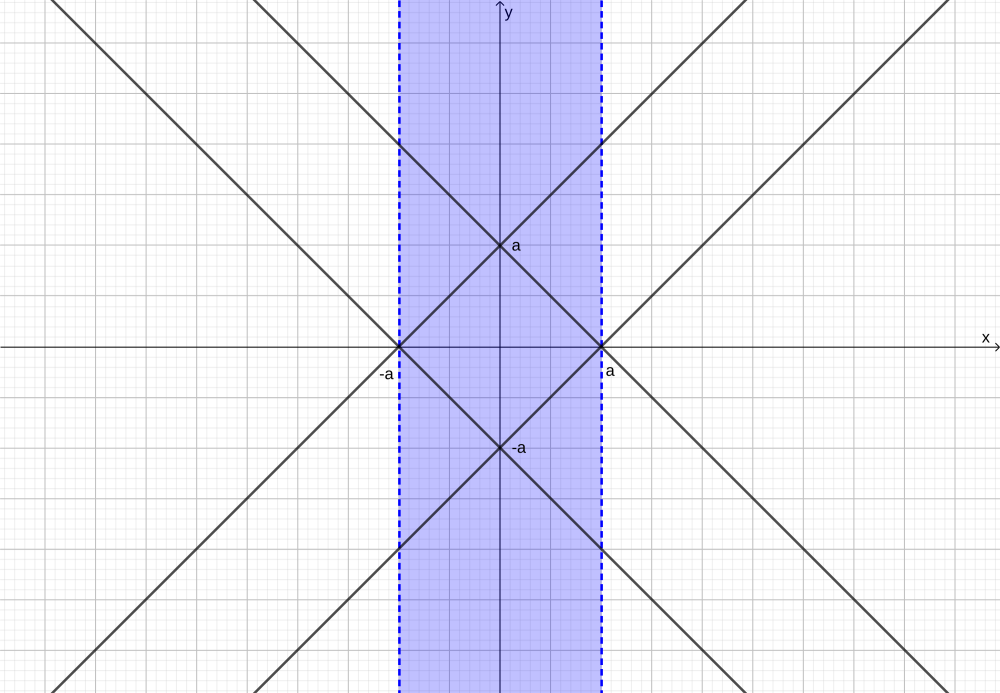
Объём этого тела будет выражаться интегралом от единицы, в котором предлы интегрирования мы поставим по рис. 1:
\[ V=\int\limits_{-a}^{0}dx\int\limits_{-a-x}^{a+x}dy\int\limits_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dz+\int\limits_{0}^{a}dx\int\limits_{x-a}^{a-x}dy\int\limits_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dz= \] \[ =\int\limits_{-a}^{0}dx\int\limits_{-a-x}^{a+x}dy2\sqrt{a^{2}-x^{2}}+\int\limits_{0}^{a}dx\int\limits_{x-a}^{a-x}dy2\sqrt{a^{2}-x^{2}}=4\int\limits_{-a}^{0}dx\sqrt{a^{2}-x^{2}}\left(a+x\right)+4\int\limits_{0}^{a}dx\sqrt{a^{2}-x^{2}}\left(a-x\right)= \] Далее в первом интеграле заменим $x=-q$, а во втором – $x=q$: \[ =-4\int\limits_{a}^{0}dq\sqrt{a^{2}-q^{2}}\left(a-q\right)+4\int\limits_{0}^{a}dq\sqrt{a^{2}-q^{2}}\left(a-q\right)=8\int\limits_{0}^{a}\sqrt{a^{2}-q^{2}}\left(a-q\right)dq= \] и разложим \[ =8a\int\limits_{0}^{a}\sqrt{a^{2}-q^{2}}dq-8\int\limits_{0}^{a}\sqrt{a^{2}-q^{2}}qdq= \] Заменим в первом из этих интегралов $q=a\sin\varphi$, второй вычисляется непосредственно: \[ =8a\int\limits_{0}^{\pi/2}\sqrt{a^{2}-a^{2}\sin^{2}\varphi}a\cos\varphi d\varphi+\left.\frac{8}{3}\left(a^{2}-q^{2}\right)^{3/2}\right|_{0}^{a}=8a^{3}\int\limits_{0}^{\pi/2}\cos^{2}\varphi d\varphi+\frac{8}{3}\left(\left(a^{2}-a^{2}\right)^{3/2}-\left(a^{2}-0^{2}\right)^{3/2}\right)= \] \[ =4a^{3}\int\limits_{0}^{\pi/2}\left(1+\cos2\varphi\right)d\varphi-\frac{8}{3}a^{3}=4a^{3}\left.\left(\varphi+\frac{1}{2}\sin2\varphi\right)\right|_{0}^{\pi/2}-\frac{8}{3}a^{3}=2\pi a^{3}-\frac{8}{3}a^{3}=\left(2\pi-\frac{8}{3}\right)a^{3}. \] Задание: № 4101, 4102.
Демидович № 4108 Найти объём тела, перейдя к сферическим/цилиндрическим координатам. Тело задано уравнением \[ \left(x^{2}+y^{2}+z^{2}\right)^{2}=a^{2}\left(x^{2}+y^{2}-z^{2}\right). \] Перейдём к сферическим координатам: \[ \left\{ \begin{array}{l} x=r\sin\theta\cos\varphi,\\ y=r\sin\theta\sin\varphi,\\ z=r\cos\theta; \end{array}\right.\quad J=r^{2}\sin\theta. \] В них уравнение примет вид \[ r^{4}=a^{2}\left(r^{2}\sin^{2}\theta-r^{2}\cos^{2}\theta\right)=a^{2}r^{2}\left(\sin^{2}\theta-\cos^{2}\theta\right)=a^{2}r^{2}\left(1-2\cos^{2}\theta\right), \] откуда следуют две возможности: \[ r_{1}=0,\quad r_{2}^{2}=a^{2}\left(1-2\cos^{2}\theta\right),\qquad\Longrightarrow\qquad r_{2}=a\sqrt{1-2\cos^{2}\theta}, \] причём чтобы последнее имело смысл, нужно чтобы \[ \frac{\pi}{2}\leqslant2\theta\leqslant\frac{3\pi}{2},\qquad\Longrightarrow\qquad\frac{\pi}{4}\leqslant\theta\leqslant\frac{3\pi}{4}. \] Пользуясь вышенайденным, расставим пределы в интеграле для объёма: \[ V=\int\limits_{0}^{2\pi}d\varphi\int\limits_{\pi/4}^{3\pi/4}d\theta\int\limits_{0}^{a\sqrt{1-2\cos^{2}\theta}}dr\left(r^{2}\sin\theta\right)= \] \[ =2\pi\int\limits_{\pi/4}^{3\pi/4}\sin\theta d\theta\int\limits_{0}^{a\sqrt{1-2\cos^{2}\theta}}r^{2}dr= \] \[ =2\pi\frac{a^{3}}{3}\int\limits_{\pi/4}^{3\pi/4}\sin\theta d\theta\sqrt{1-2\cos^{2}\theta}^{3}= \] Заменим $\cos\theta=t$, $dt=-\sin\theta d\theta$: \[ =-2\pi\frac{a^{3}}{3}\int\limits_{1/\sqrt{2}}^{-1/\sqrt{2}}\sqrt{1-2t^{2}}^{3}dt=2\pi\frac{a^{3}}{3}\int\limits_{-1/\sqrt{2}}^{1/\sqrt{2}}\sqrt{1-2t^{2}}^{3}dt= \] Теперь заменим $t=\frac{1}{\sqrt{2}}\sin\alpha$, $dt=\frac{1}{\sqrt{2}}\cos\alpha d\alpha$, $-\frac{\pi}{2}\leqslant\alpha\leqslant\frac{\pi}{2}$ \[ =2\pi\frac{a^{3}}{3}\int\limits_{-\pi/2}^{\pi/2}\sqrt{1-2\left(\frac{1}{\sqrt{2}}\sin\alpha\right)^{2}}^{3}\frac{1}{\sqrt{2}}\cos\alpha d\alpha=2\pi\frac{a^{3}}{3}\cdot\frac{1}{\sqrt{2}}\int\limits_{-\pi/2}^{\pi/2}\sqrt{1-\sin^{2}\alpha}^{3}\cos\alpha d\alpha= \] \[ =2\pi\frac{a^{3}}{3}\cdot\frac{1}{\sqrt{2}}\int\limits_{-\pi/2}^{\pi/2}\cos^{4}\alpha d\alpha=2\pi\frac{a^{3}}{3}\cdot\frac{3\pi}{8\sqrt{2}}=\frac{\pi^{2}a^{3}}{4\sqrt{2}}. \] Задание: № 4107, 4110, в обобщённо-сферических – 4112.
