Печатается по просьбе тов. Михеевой.
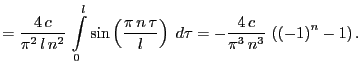
Печатается по просьбе тов. Михеевой.
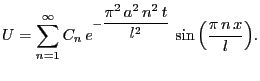
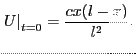
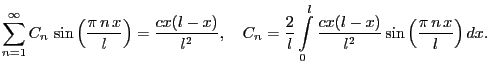
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников