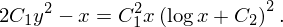Решить уравнение:
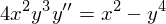 | (1) |
Проверка обобщённой однородности
Заменим в уравнении (1)
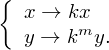
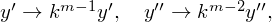 и уравнение приобретёт вид
и уравнение приобретёт вид 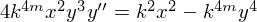 . Разделим уравнение на
. Разделим уравнение на 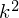 :
:
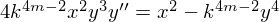 . При
. При  мы получим уравнение
мы получим уравнение 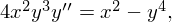 совпадающее с исходным
уравнением (1).
совпадающее с исходным
уравнением (1).
Решение
Заменим
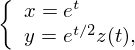 | (2) |
тогда 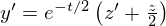 ,
, 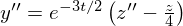 , и уравнение (1) преобразуется в такое:
, и уравнение (1) преобразуется в такое:
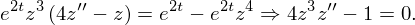
 , заменим в нём
, заменим в нём 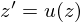 ,
, 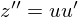 , при этом
получим
, при этом
получим
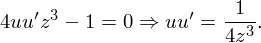
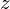 :
:
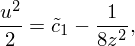
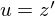 , придём к уравнению
, придём к уравнению
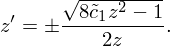
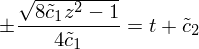
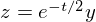 ,
, 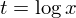 , возведём обе части в квадрат и переобозначим
, возведём обе части в квадрат и переобозначим 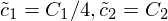 . Тогда после
несложных операций приходим к ответу
. Тогда после
несложных операций приходим к ответу