Обновились правила поведения во время контрольных работ. Прошу заранее ознакомиться.
16.03.2017
01.09.2016
14.02.2016
Все пришедшие на пересдачу дифуров погорели на одном и том же: на кратных корнях.
Посмотреть, что делать с кратными корнями в одиночных уравнениях, можно тут (на методе вариации постоянных, также применяемом в этом номере, я не настаиваю как на обязательном).
Что касается систем уравнений с кратными корнями, то там возможно два варианта действий, в зависимости от геометрической кратности этих корней. Если геометрической кратности не хватает, то действовать надо как тут или тут. Если хватает — так же, как с корнями единичной кратности, составив своё частное решение для каждого собственного вектора.
Следующая пересдача будет в понедельник, в 17:00.
26.11.2015
22.11.2015
Два объявления для первого курса
Со следующей недели допуск и отработка следующей контрольной работы будут проводиться отдельно. Отработка контрольной (т.е. возможность освободиться) будет во вторник, в 17:00. Допуск будет в субботу, в 12:00. Приходить не в своё время бессмысленно.
Вчера выяснилось, что существуют второкурсники, которые берутся помочь первокурсникам. Этот вариант, коль скоро он реализуем, лучше того, который я озвучивал вчера.
Итак, граждане с проблемами с элементарной математикой, нуждающиеся в руководстве — обращайтесь к старшим товарищам. Насколько я понял, у вас уже налажен контакт с добровольцами со второго курса и назначено время следующей встречи; у кого не налажен — обращайтесь, я налажу.
11.11.2015
Предконтрольное
Так как появились люди, думающие, что они знают, что такое правило Лопиталя, предупреждаю: за попытки решения этим методом буду ставить нули.
Постарайтесь обойтись другими способами.
10.10.2015
Тем, кто поставил сегодня tox и тем, кто это ещё сделает в будущем
Не забудьте выставить в antoxе обратно флаг «работать только по WiFi». Берегите батарею. Имейте в виду, что antox не выключается по нажатию кнопки «Назад» — для этого нужно нажать пункт «Выход» в меню.
Если в настройках зайти в пункт «Профиль», профиль экспортировать, а потом импортировать его на компьютере (например, в программе qtox) — можно с компьютера продолжать переписываться под тем же именем и с тем же контакт-листом, что на телефоне.
Antox позволяет прямо из чата включить камеру, сделать фотографию и послать снимок собеседнику. Например, можно фотографировать и пересылать ваши попытки решения, по которым у вас возникли вопросы («Досюда дорешал, а дальше не знаю»).
Компьютерная версия тох-клиента (в отличие от мобильной — но это пока) поддерживает аудио и видео-звонки. Однако звонить мне не следует — у меня всё равно не работает камера с микрофоном.
04.10.2015
Студентам из гр. 06-541, приходившим вчера
В субботу мы решили, по сути, номера 58 и 62. Тем, кто был, советую (хотя это строго необязательно) подумать над номерами 59, 60 и 61.
Также будет невредно почитать доказательства для номера 64 и номера 66 — с ними тяжеловато справиться самостоятельно.
Тов. Галимовой можно посоветовать ещё № 69 и 72.
26.04.2015
17.04.2015
Тем, кто заблудился в интегралах
Есть три основных метода решения интегралов:
- разложения,
- замены переменных (его можно применять в две стороны: замена функции на переменную и переменной на функцию),
- интегрирования по частям.
Применение этих методов иногда может быть несколько неожиданным. Но на каждый из этих методов есть свой блок примеров в Демидовиче. После решения примеров десяти из блока вы начинаете решать остальное быстро, после пятнадцати-тридцати на вас нисходит озарение и дальше вы решаете такое в уме и мгновенно. На замену — с 1674 номера (и с 1766 — ещё один блок), на разложение и иногда замену — с 1721, на интегрирование по частям — с 1791.
Большинство застрявших на середине интегралов (те, кто решили по одному интегралу — застряли в начале, так что это не для вас) не умеют именно интегрировать по частям. Что вам решать — смотрите выше.
Вне допусков вы можете задавать вопросы по тому, что у вас не получается, даже если я этого никогда не задавал.
PS Список совершенно недопустимых ошибок пополнился ещё двумя пунктами, рекомендую ознакомиться.
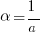 .
.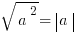 . От того и не получалось.
. От того и не получалось.