Рассмотрим ряд
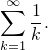
Сначала изучим свойства суммы
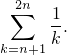
При 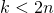 (это так для всех слагаемых, кроме последнего),
(это так для всех слагаемых, кроме последнего),
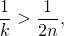
в сумме
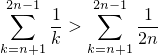
К обеим частям неравенства прибавим 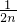 и получим, что
и получим, что
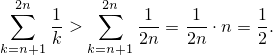
Итак,
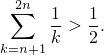
Обозначим частичные суммы изучаемого ряда, как обычно,
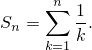
Заметим,что
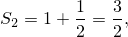
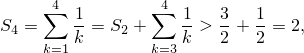
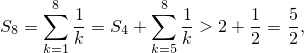
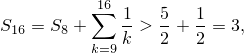
и вообще
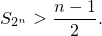 | (1) |
Доказательство этого факта методом мат. индукции было выброшено, чтобы не перегружать пост. Читателям предлагается провести его самостоятельно.
Для любого сколь угодно большого 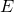 найдётся такое целое
найдётся такое целое 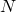 ,
что
,
что
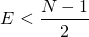
(для этого достаточно, чтобы 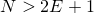 ). Но тогда, по неравенству
(1),
). Но тогда, по неравенству
(1),
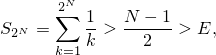
а так как слагаемые ряда положительны и частичные суммы возрастают, для
всякого 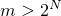
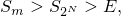
то есть последовательность сумм ряда по определению стремится к бесконечности, а не к конечному числу, что означает, что ряд расходится.
Теперь рассмотим более общий случай: ряд
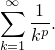 | (2) |
Выше мы рассмотрели случай 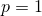 . При
. При  всё просто:
всё просто:
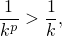
а так как меньший из этих рядов расходится, то и больший расходится. Итак,
ряд (2) расходится при всех 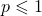 .
.
Случай 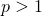 придётся рассмотреть более подробно. При
придётся рассмотреть более подробно. При 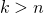
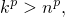
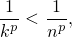
и в сумме
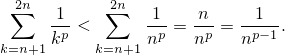 | (3) |
Воспользуемся этим неравенством, чтобы оценить сумму
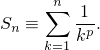
Заметим, что
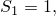
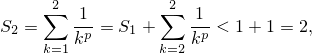
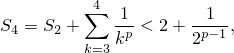
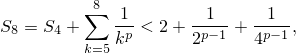
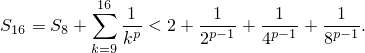
Докажем, что
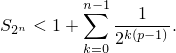 | (4) |
Для 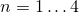 (4) уже доказано. Пусть теперь при
(4) уже доказано. Пусть теперь при 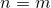 неравенство (4)
считается доказанным:
неравенство (4)
считается доказанным:
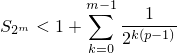
Докажем его при 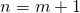 , т.е. что
, т.е. что
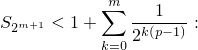
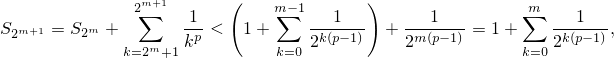
что и т.д.
Для всякого 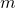 существует такое
существует такое 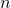 , что
, что  . В силу возрастания
. В силу возрастания
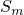 ,
,
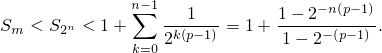 | (5) |
Но при 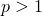 ,
,
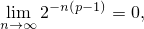
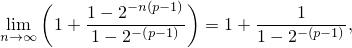
а так как сходящиеся последовательности ограничены, существует такое 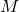 ,
что
,
что
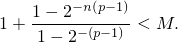
В итоге получаем, что
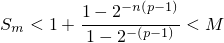
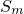 возрастает, а значит,
возрастает, а значит, 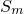 имеет предел, т.е. ряд (2) сходится.
имеет предел, т.е. ряд (2) сходится.
