Разложить функцию
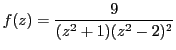 |
(1) |
в степенные ряды во всех областях комплексной плоскости.
 |
Функция  допускает четыре особых точки:
допускает четыре особых точки:  и
и
 . Области сходимости степенных рядов разложения этой функции в точке
. Области сходимости степенных рядов разложения этой функции в точке  будут ограничены окружностями с центором в начале координат и проходящими через особые точки. Таких окружностей будет две: с радиусами
будут ограничены окружностями с центором в начале координат и проходящими через особые точки. Таких окружностей будет две: с радиусами  и
и  .
.
Мы видим, что комплексная плоскость разделилась на три области, в каждой из которых  представляется разными сходящимися рядами.
представляется разными сходящимися рядами.
|
Разложим функцию  на слагаемые:
на слагаемые:
 |
(2) |
 |
Первое слагаемое имеет особые точки  и
и  . Его разложение в ряд Тейлора вокруг нуля сходится внутри малой окружности, т.е. в области I, а его разложение вокруг бесконечности сходится снаружи малой окружности, т.е. в областях II и III.
. Его разложение в ряд Тейлора вокруг нуля сходится внутри малой окружности, т.е. в области I, а его разложение вокруг бесконечности сходится снаружи малой окружности, т.е. в областях II и III.
|
 |
Второе и третье слагаемые имеют особые точки  и
и  , области сходимости их рядов ограничены большой окружностью. Их разложение в ряд Тейлора вокруг нуля сходится внутри большой окружности, т.е. в областях I и II, а их разложение вокруг бесконечности сходится снаружи большой окружности, т.е. в области III.
, области сходимости их рядов ограничены большой окружностью. Их разложение в ряд Тейлора вокруг нуля сходится внутри большой окружности, т.е. в областях I и II, а их разложение вокруг бесконечности сходится снаружи большой окружности, т.е. в области III.
|
Из вышесказанного следует, что для того, чтобы получить сходящиеся ряды для функции

, нужно:
- Для области I сложить ряды для всех трёх слагаемых, разложенных вокруг нуля;
- Для области II сложить ряды для первого слагаемого, разложенного вокруг бесконечности, и для вторых двух слагаемых, разложенных вокруг нуля;
- Для области III сложить ряды для всех трёх слагаемых, разложенных вокруг бесконечности.
Осталось получить соответствующие разложения. Для этого воспользуемся общеизвестным разложением
 |
(3) |
откуда дифференцированием обеих частей можно получить:
 |
(4) |
 |
(5) |
 |
(6) |
 |
(7) |
Тут мы будем пользоваться преобразованием

, раскладывать вокруг точки

, потом переходить обратно к

.
 |
(8) |
 |
(9) |
 |
(10) |
Теперь, используя полученное, запишем ответ для всех трёх областей. В области I
в области II
в области III
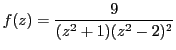

![]() на слагаемые:
на слагаемые:
















у Вас во второй формуле опечатка.
объясните мне,пожалуйста,почему при разложении функции по формуле 4 коэффициент (n+1) не учитывается?
Комментарий by Света Юматова — 20.04.2011 @ 7:28 дп
Всё поправил, теперь учитывается.
Комментарий by Shine — 20.04.2011 @ 5:55 пп