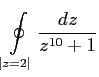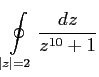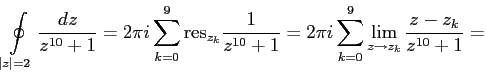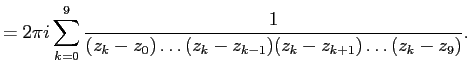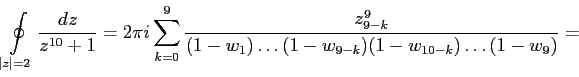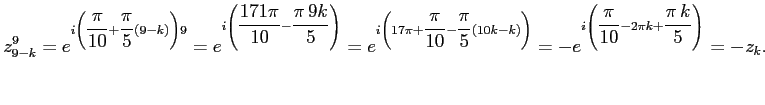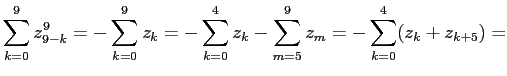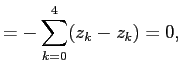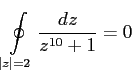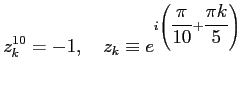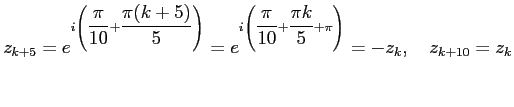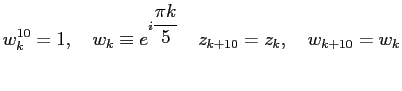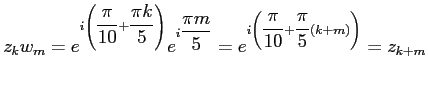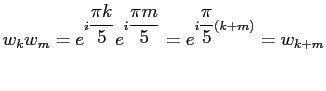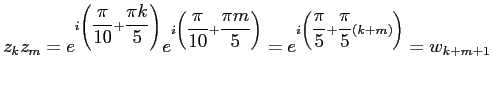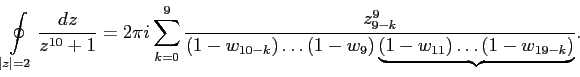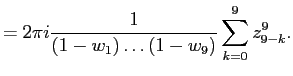Даишев, Кузнецова 8.3 « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

06.05.2010

Даишев, Кузнецова 8.3

Filed under: ТФКП — Shine @ 11:47 пп

Найти значение интеграла:

$\displaystyle \oint\limits_{\vert z=2\vert}\frac{dz}{z^{10}+1}$

Судя по всему, авторы имели в виду такой интеграл:

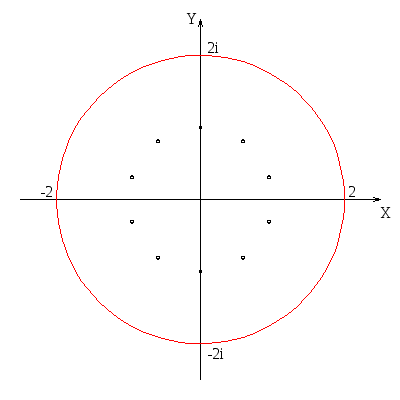
$\displaystyle \oint\limits_{\vert z\vert=2}\frac{dz}{z^{10}+1}$

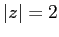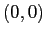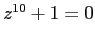Уравнение $\vert z\vert=2$ задаёт окружность с центром в точке $(0,0)$ и радиусом 2. Особые точки подынтегрального выражения определяются из уравнения $z^{10}+1=0$ . Оно даёт десять корней, каждый из которых имеет кратность 1. Следовательно, каждый из корней является полюсом первого порядка. Обозначим их и приведём некоторые их свойства, легко получаемые из определения:

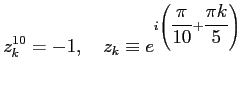$\displaystyle z_k^{10}=-1,\quad z_k\equiv e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi k}{5}\right)}$

(1)

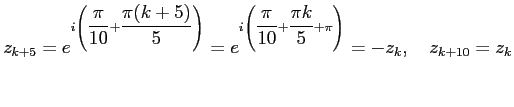$\displaystyle z_{k+5}=e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi (k+5)}{5}\right)}= e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi k}{5}+\pi\right)}=-z_k,\quad z_{k+10}=z_k$

(2)

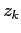
Все точки $z_k$ входят в область, ограниченную контуром. Вычеты в них вычисляются по формуле

$\displaystyle \mathrm{res}_{a}f(z)=\lim\limits_{z\to a}f(z)(z-a).$

Также нам пригодится обозначение для корней десятой степени единицы:

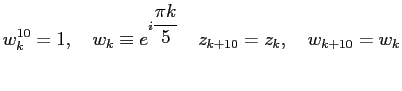$\displaystyle w_k^{10}=1,\quad w_k\equiv e^{i\dfrac{\pi k}{5}}\quad z_{k+10}=z_k,\quad w_{k+10}=w_k$

(3)

Умножаются эти числа по следующим правилам:

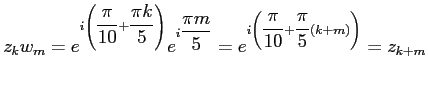$\displaystyle z_kw_m= e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi k}{5}\right)} e^{i\dfrac{\pi m}{5}}= e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi}{5}(k+m)\right)}= z_{k+m}$

(4)

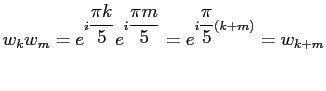$\displaystyle w_kw_m= e^{i\dfrac{\pi k}{5}} e^{i\dfrac{\pi m}{5}}= e^{i\dfrac{\pi}{5}(k+m)}= w_{k+m}$

(5)

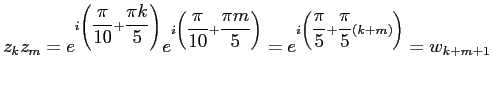$\displaystyle z_kz_m= e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi k}{5}\right)} e^{i\... ...5}\right)} = e^{i\left(\dfrac{\pi}{5}+ \dfrac{\pi }{5}(k+m)\right)} = w_{k+m+1}$

(6)

По теореме о вычетах, раскладывая знаменатель на множители получим:

$\displaystyle \oint\limits_{\vert z\vert=2}\frac{dz}{z^{10}+1}= 2\pi i\sum\limi... ...}= 2\pi i\sum\limits_{k=0}^{9}\lim \limits_{z\to z_k}\frac{z - z_k}{z^{10}+1}=$

$\displaystyle =2\pi i\sum\limits_{k=0}^{9}\frac{1}{(z_k-z_0)\ldots(z_k-z_{k-1})(z_k-z_{k+1})\ldots(z_k-z_{9})}.$

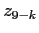
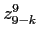
Умножим каждую скобку в знаменателе на $z_{9-k}$ . Для сохранения равенства умножим числитель на $z_{9-k}^9$ . По формуле (6) получим

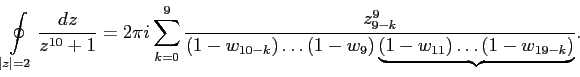$\displaystyle \oint\limits_{\vert z\vert=2}\frac{dz}{z^{10}+1}= 2\pi i\sum\limi... ...z_{9-k}^9}{(1-w_{10-k})\ldots(1-w_9)\underbrace{(1-w_{11})\ldots(1-w_{19-k})}}.$

(7)

Применим (3) и поменяем местами выделенные множители в знаменателе с невыделенными:

$\displaystyle \oint\limits_{\vert z\vert=2}\frac{dz}{z^{10}+1}= 2\pi i\sum\limi... ...k=0}^{9}\frac{z_{9-k}^9}{(1-w_{1})\ldots(1-w_{9-k})(1-w_{10-k})\ldots(1-w_9)}=$

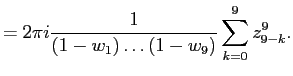$\displaystyle =2\pi i\frac{1}{(1-w_{1})\ldots(1-w_9)}\sum\limits_{k=0}^{9}z_{9-k}^9.$

(8)

Рассмотрим теперь судьбу последнего слагаемого. Согласно (1)

$\displaystyle z_{9-k}^9= e^{i\left(\dfrac{\pi}{10}+ \dfrac{\pi }{5}(9-k)\right)... ...\right)}= -e^{i\left(\dfrac{\pi}{10}- 2\pi k +\dfrac{\pi\,k}{5}\right)}= -z_k.$

Тогда по (2)

$\displaystyle \sum\limits_{k=0}^{9}z_{9-k}^9= -\sum\limits_{k=0}^{9}z_k= -\sum\... ...ts_{k=0}^{4}z_k-\sum\limits_{m=5}^{9}z_m= -\sum\limits_{k=0}^{4}(z_k+z_{k+5})=$