А могли и не заменять ничего, а использовать формулу, которую пытался вспомнить Кондрат:
Тогда
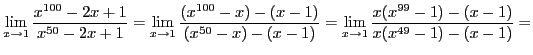
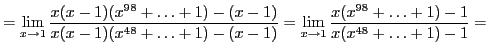
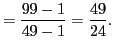
А могли и не заменять ничего, а использовать формулу, которую пытался вспомнить Кондрат:
Тогда
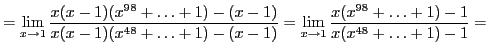
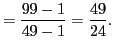
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников