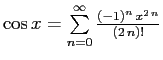 , представим функцию
, представим функцию
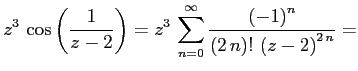
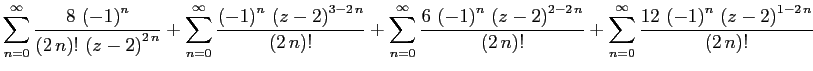
Для того, чтобы найти вычет в точке
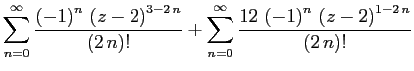
В первой сумме такое слагаемое соответствует
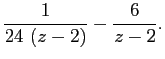
Если привести их к общему знаменателю, коеффициентом при
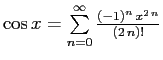 , представим функцию
, представим функцию
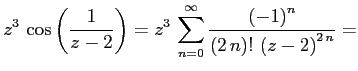
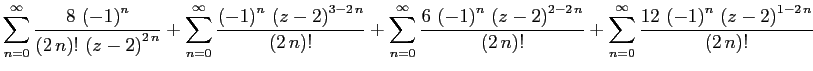
Для того, чтобы найти вычет в точке
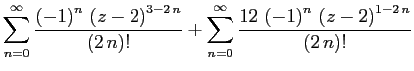
В первой сумме такое слагаемое соответствует
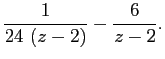
Если привести их к общему знаменателю, коеффициентом при
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников