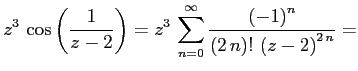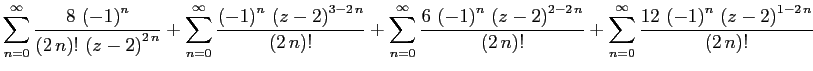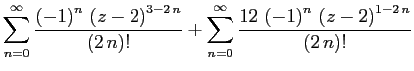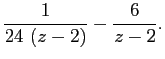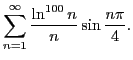Май « 2011 « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

13.05.2011

Контрольные по ТФКП у 2го курса

Filed under: кто что где когда — Shine @ 12:41 пп

будут на следующей неделе, по интегралам и операционному исчислению. Соответственно, гр. 692 пишет 18 мая, гр. 697 — 21 мая. 25 и 28 мая можно будет переписать наиболее неудавшиеся работы. Список людей, которые будут иметь такую возможность, будет вывешен отдельно.

Пользоваться на контрольных, как обычно, ничем будет нельзя. Рекомендуется начать учить заранее.

Comments (0)

12.05.2011

Даишев, Кузнецова 8.32

Filed under: ТФКП — Shine @ 12:57 дп

Вычислить интеграл

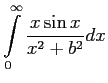
$\displaystyle \int\limits_0^{\infty}\frac{x\sin x}{x^2+b^2}dx$

(1)

(предполагается, что $b\in \mathbb{R}$ ).

(more…)

Comments (0)

11.05.2011

Даишев, Кузнецова 7.10

Filed under: ТФКП — Shine @ 1:20 дп

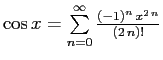Очевидно, что единственная кроме бесконечности особая точка функции $f(z)=z^3\,\cos\left(\frac{1}{z-2}\right)$ - это $z=2$ . Используя известное разложение косинуса $\cos x=\sum\limits_{n=0}^{\infty }{{\frac{\left(-1\right)^{n}\,x^{2\,n}}{ \left(2\,n\right)!}}}$ , представим функцию $f(z)$ так:

$\displaystyle z^3\,\cos \left({\frac{1}{z-2}}\right)= z^3\,\sum_{n=0}^{\infty }{ {\frac{\left(-1\right)^{n}}{\left(2\,n\right)!\,\left(z-2\right)^{2 \,n}}}}=$

$\displaystyle \sum_{n=0}^{\infty }{{\frac{8\,\left(-1\right)^{n}}{\left(2\,n \... ...ac{12\,\left(-1 \right)^{n}\,\left(z-2\right)^{1-2\,n}}{\left(2\,n\right)!}}}$

Для того, чтобы найти вычет в точке $z=2$ , надо из этих сумм выбрать слагаемые, имеющие множитель $(z-2)^{-1}$ . Первая и третья из этих сумм содержат только слагаемые с целыми степенями $(z-2)$ , следовательно, нужные нам слагаемые есть только в этих суммах:

$\displaystyle \sum_{n=0}^{\infty }{{\frac{\left(-1 \right)^{n}\,\left(z-2\righ... ...ac{12\,\left(-1 \right)^{n}\,\left(z-2\right)^{1-2\,n}}{\left(2\,n\right)!}}}$