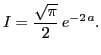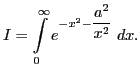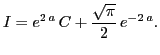Вспомним интеграл Эйлера-Пуассона
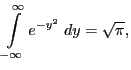
и произведём в нём замену
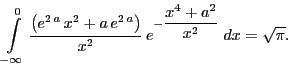
После раскрытия скобок и замены
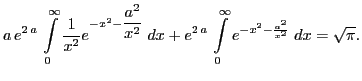
Далее продифференцируем (1) и учтём результат в предыдущем равенстве:
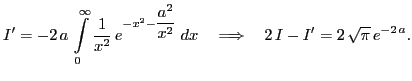
Последнее есть неоднородное дифференциальное уравнение первого порядка. После стандартной для таких уравнений процедуры решения получим
Для нахождения ![]() заменим
заменим ![]() на интеграл по определению (1) и положим
на интеграл по определению (1) и положим ![]() :
:
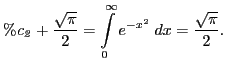
Так как из предыдущего ![]() , уравнение (2) приводит к окончательному результату:
, уравнение (2) приводит к окончательному результату: