Найти площадь фигуры 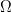 , ограниченной графиком уравнения:
, ограниченной графиком уравнения:
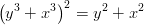 | (1) |
при 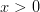 и
и 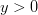 , перейдя к полярным координатам.
, перейдя к полярным координатам.
Произведём замену координат на полярные




 | (2) |

Площадь фигуры  находится по формуле
находится по формуле

 в первой четверти будет такой, как изображено на рисунке, в полярных координатах
интеграл из этой формулы запишем так:
в первой четверти будет такой, как изображено на рисунке, в полярных координатах
интеграл из этой формулы запишем так:







