Найти площадь фигуры  , ограниченной графиком уравнения:
, ограниченной графиком уравнения:
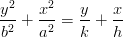 | (1) |
перейдя к обобщённым полярным координатам.
В этой задаче в обобщённых полярных координатах оставим  в первой степени:
в первой степени:
 | (2) |
Тогда уравнение (1) станет таким (как  обозначим координату точек на границе области
обозначим координату точек на границе области
 ):
):



 находится по формуле
находится по формуле

 возможно по тем областям, в которых
возможно по тем областям, в которых  , поэтому в обобщённых полярных
координатах
, поэтому в обобщённых полярных
координатах


