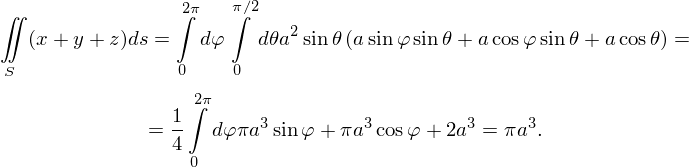Вычислить поверхностный интеграл 1-го рода:
 | (1) |
где  – поверхность
– поверхность
 | (2) |
Зададим поверхность в параметрическом виде. В сферических координатах уравнение поверхности (2) записывается
как 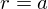 , и если перейти обратно в декартовы координаты, получится:
, и если перейти обратно в декартовы координаты, получится:
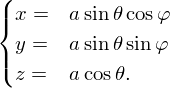 | (3) |
Компоненты 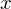 ,
, 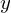 и
и 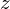 радиус-вектора
радиус-вектора 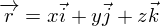 , таким образом, зависят от двух параметров, которые для
верхней полусферы лежат в следующих областях:
, таким образом, зависят от двух параметров, которые для
верхней полусферы лежат в следующих областях: 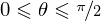 и
и 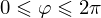 .
.
После параметризации
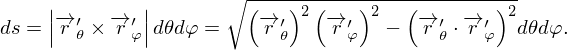 | (4) |
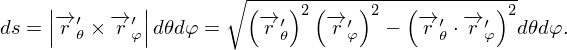
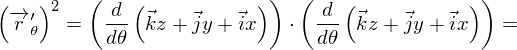

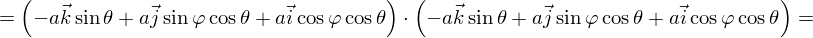
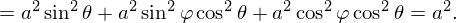
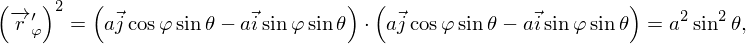
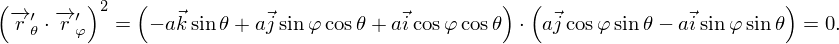
Тогда 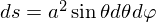 . Подставляем
. Подставляем 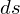 и (3) в интеграл (1):
и (3) в интеграл (1):