Страница сетевой поддержки учеников Тимура Юрьевича Альпина

В качестве компенсации за сорванное сегодня занятие могу объяснить одно старое домашнее задание.

Номер 66. Доказать, что

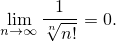
Для любого ε > 0 можно вычислить E = -log ₂ε. Мы рассмотрим сначала

(1)

Для любого же такого E можно найти целое

(2)

Основываясь на этом неравенстве, можно доказать многое.

1. Заметим, что в силу (1), m ≥ 3. Для таких m

   а в силу (2),

   

2. Так как в этой сумме k > m, то log ₂k > log ₂m > E, а значит,

   где – это количество слагаемых в сумме.

3. Из (2) следует, что log ₂m² > 2E. А отсюда

   где p – любое натуральное число.

Теперь сопоставим полученное. Любое целое n > m² + m можно представить в виде n = m² + m + p. Тогда

т.е.

Итак, log ₂ > -log ₂ε, а значит, -log ₂ < log ₂ε. Применяя к обеим частям возрастающую функцию f(x) = 2^x, мы получим, что

Напомню, что это верно для любого n > m² + m. Отсюда следовало бы по определению, что стремится к нулю, если бы мы рассмотрели все ε > 0. Но мы пока рассмотрели только ε < .

Пусть теперь ε ≥. Для него всегда можно найти ε₁ < ≤ ε. Согласно вышедоказанному, для ε₁ найдётся N = m² + m (где m – целое, большее ), что при n > N будет < ε₁ < ε, следовательно < ε. Значит, для любого n можно найти такое N, после которого < ε, что по определению означает

.