Восстановить аналитическую функцию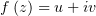 
, про которую известно,
что она:
1) Имеет мнимую часть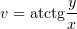 
,
2) Имеет известное значение в некоторой точке: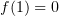 
.
Об аналитической функции мы знаем, что
 | (1) |
Воспользовавшись первым уравнением и подставиви в него известное 
,
получим 
:
Проинтегрируем обе части полученного по 
, и получим 
с точностью до
произвольной функции от 
:
 | (2) |
Для определения ч воспользуемся вторым уравнением из условий (1):
откуда
На этот раз нами добавляется к первообразной константа (а не, например,
фукнция от 
), ибо 
, в отличиче от 
, есть функция одной переменной.
В силу (2),
Тогда мы можем определить функцию с точностью до постоянного действительного слагаемого.
Зная значение функции в единице, мы сможем это слагаемое определить:
Что за функция у нас получилась? Мы знаем, что при 
,
при этом 
, 
при 
и 
при 
. Сравнив полученную функцию с логарифмом аргумента в
алгебраической форме, придём к выводу, что в правой полуплоскости
(
) мы получили главную ветвь логарифма (при 
). В левой
полуплоскости
но, по-прежнему,
Значит, там
Окончательный ответ запишем так:
При 
функция не определена.
