Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром, не требующее забитой формулами головы « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

11.12.2013

Filed under: ВИиИУ,Решения — Shine @ 5:16 пп

Решить уравнение:

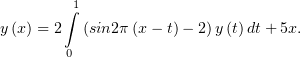
∫1 y(x) = 2 (sin2π(x − t)− 2)y (t)dt+ 5x. 0

После разложения синуса разности в ядре на слагаемые уравнение примет вид:

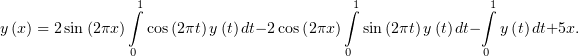
1 1 1 ∫ ∫ ∫ y(x) = 2sin(2πx) cos(2πt)y(t)dt− 2cos(2πx) sin (2πt)y (t)dt− y(t)dt+5x. 0 0 0

Введя константы

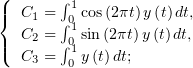( ∫1 |{ C1 = ∫0 cos(2πt)y(t)dt, | C2 = ∫10 sin(2πt)y (t)dt, ( C3 = 10 y (t)dt;

(1)

выразим через них 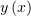$y (x)$ :

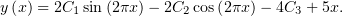y(x) = 2C1sin (2πx )− 2C2cos(2πx)− 4C3 + 5x.

(2)

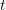Заменив $x$ на $t$ , подставим 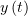$y(t)$ в таком виде в (1):

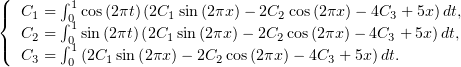
( ∫1 |{ C1 = ∫01 cos(2πt)(2C1 sin (2πx) − 2C2cos(2πx)− 4C3 +5x) dt, | C2 = ∫0 sin (2πt)(2C1 sin(2πx)− 2C2 cos(2πx )− 4C3 + 5x)dt, ( C3 = 10 (2C1sin(2πx)− 2C2 cos(2πx) − 4C3 + 5x)dt.

Вычислив интегралы в этих уравнениях, получим формулы:

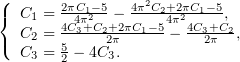
( { C1 = 2πC12−5− 4π2C2+22πC1−-5, C2 = 4C4π3+C2+2πC1−-54π− 4C3+C2, ( C3 = 5 − 4C23π. 2π 2

Решая эту систему, получим 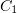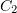$C1$ , $C2$ и $C3$ :

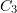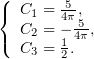
( { C1 = 54π, C2 = −45π, ( C3 = 12.

Подставив найденные значения в (2), получим окончательный ответ:

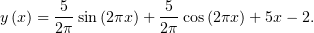
5 5 y(x) = --sin (2πx)+ ---cos(2πx )+ 5x− 2. 2π 2π

Как видите, тут вполне достаточно знать формулы, не выходящие за пределы программы первого курса, и общее направление движения.

No comments yet.

Для отправки комментария вам необходимо авторизоваться.