Решение однородного уравнения Фредгольма второго рода « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

11.12.2013

Решение однородного уравнения Фредгольма второго рода

Filed under: ВИиИУ,Решения — Shine @ 6:50 пп

Найти ненулевые решения уравнения (этого уравнения нет в задачнике):

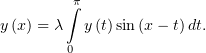∫π y (x) = λ y (t)sin (x− t)dt. 0

(1)

Разложив синус и обозначив константы

{ ∫π C1 = ∫0π y (t)cos(t)dt, C2 = 0 y (t)sin (t)dt,

выразим

y(x) = C1λsin (x)− C2λcos(x)

(2)

и получим на эти константы систему уравнений (подробности см. в предыдущем номере):

{ − πλC2− C1 = 0, πλ2C1− C2 = 0. 2

В матричном виде эту систему можно представить так:

( ) ( ) − 1 − πλ2 C1 πλ2 − 1 C2 = 0.

Ненулевые решения эта система (если подставить нулевое в (2), получится $y (x) = 0$ ) будет иметь только при

( πλ ) det − 1 − -2 = 0, πλ2 − 1

т.е.

2i λ = π-.

(3)

При $λ = 2i∕π$ , $C2 = − iC1$ . Тогда

2C1 y (x) = -π--(cos(x)− isin (x)).

(4)

Аналогично при $λ = − 2i∕π$ , $C2 = iC1$ . Тогда

y (x) = 2C1-(cos(x)+ isin (x)). π

(5)

Обобщая полученное, можно сказать, что действительных ненулевых решений уравнение (1) не имеет ни при каком значении $λ$ , но при (3) существуют решения (4) и (5) соответственно.