Про эллиптические уравнения всем группам, кроме 06-206, я не привёл никаких обоснований, а группе 06-206 наговорил общих слов. Вероятно, вам всё ещё интересно, почему описанные мной действия с ними дают неизменно превосходный результат.
Итак, мы заменяем в уравнении
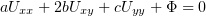
свободные аргументы  и
и 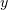 на
на  и
и 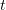 , и получаем уравнение аналогичного
вида:
, и получаем уравнение аналогичного
вида:
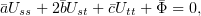 | (1) |
где

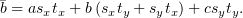 | (2) |
Пытаясь занулить  , мы пришли к уравнению
, мы пришли к уравнению
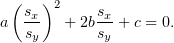
Оказалось, что 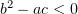 , и мы нашли такие
, и мы нашли такие 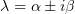 , что
, что
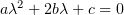 . Если рассмотреть вариант
. Если рассмотреть вариант 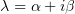 (для
(для
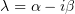 получается аналогично) и раскрыть скобки, получится
получается аналогично) и раскрыть скобки, получится
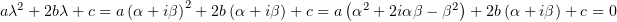 .
Или, если разложить покомпонентно и уравнение с комплексной частью
поделить пополам,
.
Или, если разложить покомпонентно и уравнение с комплексной частью
поделить пополам,
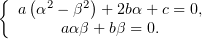 | (3) |
Положим теперь, что мы для найденного 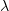 решили уравнение
решили уравнение 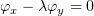 ,
нашли комплексное решение
,
нашли комплексное решение 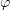 , а далее обозначили его действительную и
мнимую часть как
, а далее обозначили его действительную и
мнимую часть как  и
и 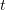 :
: 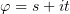 . Уравнение на
. Уравнение на 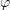 приобретает тогда
такой вид:
приобретает тогда
такой вид:
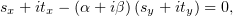
или
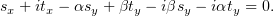
Так как комплексное число равно нулю только тогда, когда нулевыми
являются обе его части, мы можем выразить 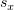 и
и 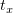 :
:
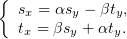
Выполним эту подстановку в 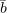 , определённом в (2):
, определённом в (2):
![╞b = a(αsy - βty)(βsy + αty)+ b[(αsy - βty)ty + sy(βsy +αty)]+ csyty =](http://shine.ylsoftware.com/math-img/ellip_parab2/ellip_parab230x.png)
![2 2 [ ( 2 2) ]
= sy(aαβ + bβ)+ ty(- aα β - bβ)+ syty a α - β + 2bα + c =](http://shine.ylsoftware.com/math-img/ellip_parab2/ellip_parab231x.png)
![( ) [ ( ) ]
s2y - t2y (aα β + bβ)+ syty a α2 - β2 + 2bα + c .](http://shine.ylsoftware.com/math-img/ellip_parab2/ellip_parab232x.png)
Оба слагаемых равны нулю согласно (3), значит, как и было сказано,
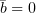 .
.
Для параболических уравнений тоже существует возможность избавиться от
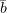 . Напомню, что
. Напомню, что  в этом случае находится из уравнения
в этом случае находится из уравнения 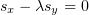 , что
позволяет заменить
, что
позволяет заменить 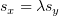 :
:
![╞
b = aλsytx +b (λsyty + sytx)+ csyty = sy [tx(aλ+ b)+ ty(bλ+ c)].](http://shine.ylsoftware.com/math-img/ellip_parab2/ellip_parab238x.png)
Вспомним теперь, что для параболических уравнений 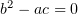 ,
значит
,
значит
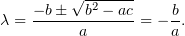
Подставив это значение, получим, что
![[ ( ) ( ) ] [ ]
╞b = s t - ab + b + t - b2 + c = s t (- b+ b)- ty(b2 - ac) = s [t ⋅0- t ⋅0] = 0.
y x a y a y x a y x y](http://shine.ylsoftware.com/math-img/ellip_parab2/ellip_parab241x.png)
В результате мы добьёмся того, что 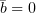 и в уравнении (1) останется только
одна вторая производная –
и в уравнении (1) останется только
одна вторая производная – 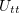 .
.
