Страница сетевой поддержки учеников Тимура Юрьевича Альпина

20.02.2015

Площадь сектора

Filed under: мат. ан. сем. 2,пепел,Решения — Shine @ 6:39 пп

Я не успел вывести формулу для площади криволинейного сектора. Выкладываю этот вывод, заодно напомню его начало в более понятном виде. Кто хорошо понял начало вывода - те могут начинать читать с формулы (1).

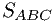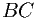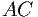Требуется найти площадь сектора SABC . Она ограничена отрезками BC и AC , и отрезком графика функции 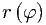r(φ) , построенного в полярных координатах.

Легко будет найти площадь другой фигуры:

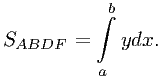
∫b SABDF = ydx. a

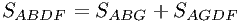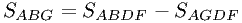Заметим, что SABDF = SABG + SAGDF , значит SABG = SABDF − SAGDF . Тогда искомое можно представить так:

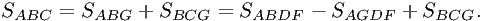
SABC = SABG + SBCG = SABDF − SAGDF + SBCG.

Используя, что

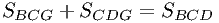
SBCG + SCDG = SBCD

и

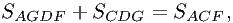
S +S = S , AGDF CDG ACF

добавим и вычтем 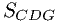SCDG и представим

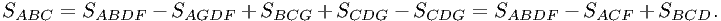
SABC = SABDF − SAGDF +SBCG +SCDG − SCDG = SABDF − SACF + SBCD.

Найдём по-отдельности всё нужное. В полярных координатах

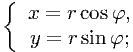
{ x = rcosφ, y = rsinφ;

и мы можем преобразовать

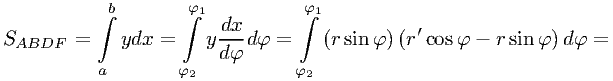
∫b ∫φ1 φ∫1 dx- ′ SABDF = ydx = y dφdφ = (rsin φ)(r cosφ − rsinφ)dφ = a φ2 φ2

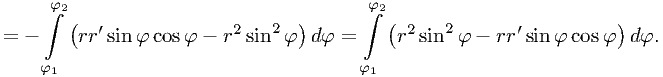
∫φ2 φ∫2 ( ′ 2 2 ) ( 2 2 ′ ) = − rr sin φcosφ − r sin φ dφ = r sin φ − rrsinφ cosφ dφ. φ1 φ1

Теперь выразим

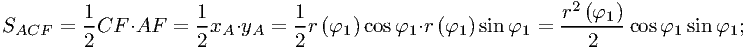
1 1 1 r2(φ ) SACF = -CF ⋅AF = -xA⋅yA = -r(φ1)cosφ1⋅r (φ1 )sinφ1 = ----1-cosφ1 sinφ1; 2 2 2 2

Аналогично

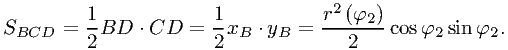
1 1 r2(φ2) SBCD = 2BD ⋅CD = 2xB ⋅yB = --2---cosφ2sinφ2.

С учётом всего этого,

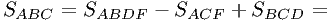SABC = SABDF − SACF + SBCD =
(1)

φ∫2 ( 2 2 ′ ) r2(φ1) r2(φ2) = r sin φ − rr sinφ cosφ dφ− 2 cosφ1 sinφ1+ 2 cosφ2 sinφ2 = φ1

φ2 | ∫ (2 2 ′ ) r2(φ) ||φ2 = r sin φ − rrsinφ cosφ dφ + 2 cosφ sinφ |φ . φ1 1

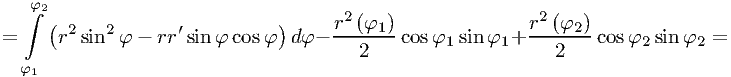
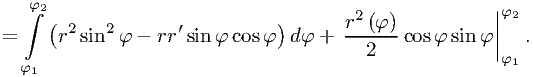
Преобразуем второе слагаемое:

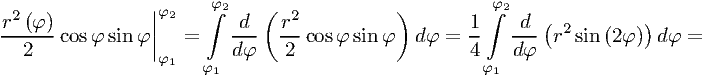
2 |φ2 ∫φ2 ( 2 ) ∫φ2 r-(φ-)cosφsinφ|| = d-- r- cosφ sin φ dφ = 1 d-(r2sin(2φ))dφ = 2 |φ1 φ dφ 2 4φ dφ 1 1

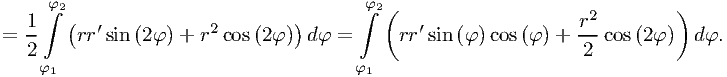
1 φ∫2( ′ 2 ) φ∫2( ′ r2 ) = 2 rrsin(2φ)+ r cos(2φ) dφ = rr sin (φ) cos(φ) + 2-cos(2φ) dφ. φ1 φ1

Тогда

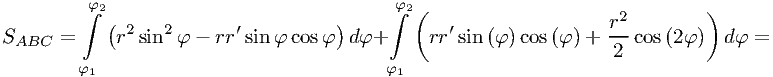
φ φ ∫ 2( 2 2 ′ ) ∫ 2( ′ r2 ) SABC = r sin φ− rr sin φcosφ dφ+ rr sin(φ)cos(φ)+ -2 cos(2φ ) dφ = φ1 φ1

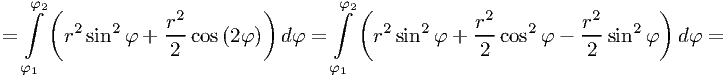
φ2 φ2 ∫ ( 2 2 r2 ) ∫ ( 2 2 r2 2 r2 2 ) = r sin φ + 2 cos(2φ) dφ = r sin φ + 2 cos φ − 2 sin φ dφ = φ1 φ1

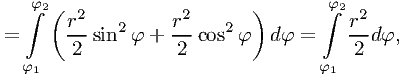
φ φ ∫ 2(r2 2 r2 2 ) ∫2r2 = -2 sin φ + 2-cos φ dφ = -2 dφ, φ1 φ1

что и требовалось доказать.

Комментариев нет »

No comments yet.

RSS feed for comments on this post.

Leave a comment

Для отправки комментария вам необходимо авторизоваться.

Хостингом угостил Вадим "Moose" Калинников