Страница сетевой поддержки учеников Тимура Юрьевича Альпина

17.04.2015

Даишев, Никитин №100

Filed under: ММФ,Решения — Shine @ 3:06 пп

Разложить единицу в ряд по функциям Бесселя с индексом 0 на интервале x ∈ [0,l] , т.е. представить её в виде

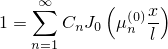∞∑ ( (0)x) 1 = CnJ0 μn l n=1
(1)

Мы будем пользоваться свойством ортогональности функций Бесселя

∫l J (μ(m)x) J ( μ(m )x)xdx = δ l2[J′ (μ(m))]2 m n l m k l kn2 m n 0
(2)

для уничтожения суммы в правой части (1). Умножим обе части (1) на ( (0)x) J0 μk l x

( (0)x) ∑∞ ( (0)x) ( (0)x-) J0 μk l x = CnJ0 μn l J0 μk l x n=1

и проинтегрируем по x по отрезку [0,l]

∫l ( ) ∫l ∞∑ ( ) ( ) J0 μ(k0)x- xdx = CnJ0 μ (0n)x- J0 μ(k0)x- xdx. 0 l 0 n=1 l l
(3)

Преобразуем части этого соотношения отдельно. Правая часть:

∫l∑∞ ( x ) ( x) ∑∞ ∫l ( x ) ( x) ∑∞ l2[ ( ) ]2 CnJ0 μ(n0)-- J0 μ(0k)-- xdx = Cn J0 μ(n0)-- J0 μ (0k)-- xdx = Cnδkn-- J′0 μ(n0) = 0 n=1 l l n=1 0 l l n=1 2

По формуле (1) из методички J′0(x) = − J1(x) , так что

l2- 2( (0)) = Ck 2J 1 μk .

Левая часть: заменим (0)x μk l = t , l x = μ(0k)t

∫l ( )2 μ∫(0k) J ( μ(0)x) xdx = -l-- J (t)tdt = 0 k l μ(0) 0 0 k 0

По формуле (2) из методички J (x) = 1J (x )+ J′(x) 0 x 1 1

( )2 μ∫(0k)( ) ( )2 ( μ∫(k0) μ∫(0k) ) = -l-- 1J (t)+ J′(t) tdt = -l-- | J (t)dt + J ′(t)tdt| = μ(0k) t 1 1 μ(k0) ( 1 1 ) 0 0 0

интегрируем по частям

( (0) (0) ) ( l )2 μ∫k μ(0) μ∫k ( l )2 ( ) l2 ( ) = -(0)- |( J1 (t)dt+ J1 (t)t|0k − J1(t)tdt|) = -(0)- J1 μ (0k) μ(k0)= -(0)J1 μ(k0) . μk 0 0 μk μk

Итого (3) превращается в

l2 2( (0)) l2 ( (0)) Ck 2J 1 μk = -(0)J1 μk , μk

1 ( (0)) -1-- Ck 2J1 μk = μ(0), k

C = -----2(---)-. k μ(0)J1 μ(0) k k

Подставив это в (1), получим такое разложение единицы:

∑∞ ( x) ∞∑ 2 ( x) 1 = CnJ0 μ(n0)l- = -(0)--(-(0))J0 μ(0n)l- . n=1 n=1μn J1 μn

Комментариев нет »

No comments yet.

RSS feed for comments on this post.

Leave a comment

Для отправки комментария вам необходимо авторизоваться.

Хостингом угостил Вадим "Moose" Калинников