Задача на объём — в помощь тем, кто разбирается с телами вращения.
Найти объём тела, полученного при вращении кривой \begin{equation} x^{2}-xy+y^{2}=a^{2}\label{main} \end{equation} вокруг оси $Ox$.
Нередко бывает, что кратко формулируемая задача имеет долгое и тяжёлое решение и доставляет массу проблем на ровном месте. В аудитории такие задачи решать некогда, дома их, как правило, не осиливают, а знать о них надо. И вот, появился хороший повод такие задачи поразбирать.
Заметим, что уравнение в нашем номере, вроде бы короткое и простое, не только не является каноническим уравнением какой-либо кривой второго порядка, но и не приводится к таковому без поворотов.
При повороте координатных осей на угол $\alpha$ координаты $x'$ и $y'$ в новой системе связаны с координатами $x$ и $y$ в старой по такому закону: \begin{equation} \left\{ \begin{array}{l} x=x'\cos\alpha-y'\sin\alpha,\\ y=x'\sin\alpha+y'\cos\alpha. \end{array}\right.\label{perehod} \end{equation} Подставив эти замены в уравнение (\ref{main}) и собрав слагаемые с одинаковыми степенями координат, получим \begin{equation} \left(1-\sin\alpha\cos\alpha\right)x'^{2}+\left(2\sin^{2}\alpha-1\right)x'y'+\left(1+\sin\alpha\cos\alpha\right)y'^{2}=a^{2}.\label{povernuli} \end{equation} Из этого уравнения исчезнет $x'y'$, если \[ 2\sin^{2}\alpha-1=0, \] \[ \sin\alpha=\frac{1}{\sqrt{2}},\qquad\alpha=\frac{\pi}{4}. \] Полученное решение для $\alpha$, конечно, не единственное, но нас устроит любое из решений. Подставим полученное $\alpha$ в (\ref{povernuli}) \[ \left(1-\frac{1}{2}\right)x'^{2}+\left(1+\frac{1}{2}\right)y'^{2}=a^{2}, \] \[ \frac{x'^{2}}{2}+\frac{3y'^{2}}{2}=a^{2}. \] Легко заметить, что в координатах $x'$ и $y'$ последнее уравнение описывает эллипс с полуосями $\sqrt{2}$ и $\sqrt{\frac{2}{3}}$, изображённый на рис. 1 (синяя линия).
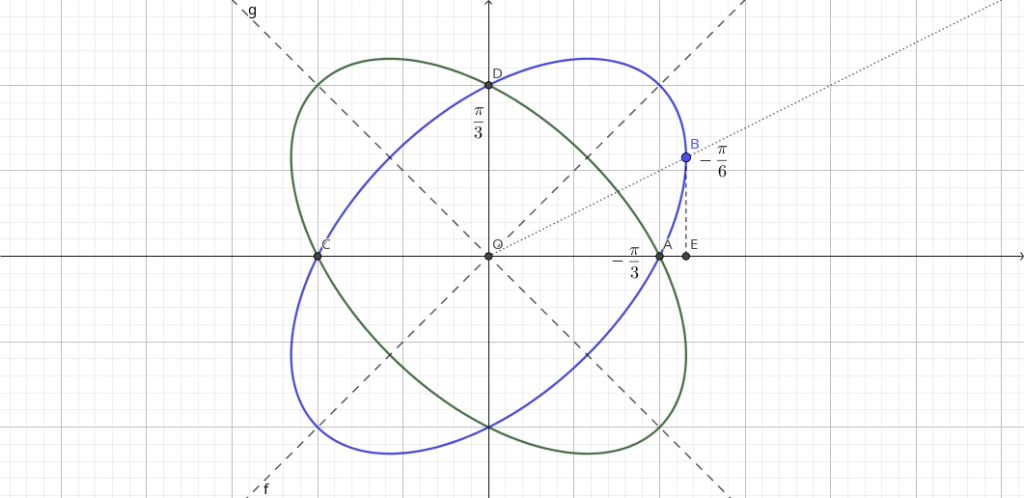
Если этот эллипс вращать вокруг оси $Ox$, он опишет фигуру на рис. 2, ещё раз пересёкшись с плоскостью $xy$ (по серой линии на рис. 1) после полуоборота.
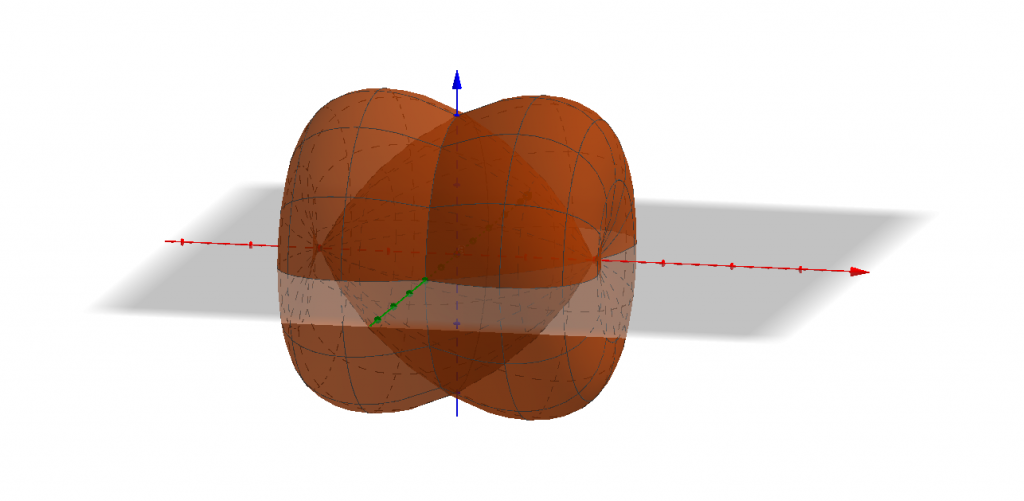
Так как серая линия получена поворотом вокруг оси $Ox$, её уравнение можно получить заменой в исходном уравнении $y$ на $-y$: \[ x^{2}+xy+y^{2}=a^{2} \] Однако то же самое получится, если заменить $x$ на $-x$. Тело вращения исходной кривой получится таким же, как если бы мы вращали объединённую сине-серую кривую на рис. 1. При этом последняя симметрична относительно оси $Oy$ (каждой точке синей кривой справа соответствует точка серой кривой слева, и наоборот), следовательно, тело вращения симметрично относительно плоскости $yz$. Поэтому для нахождения его объёма мы найдём объём правой части и умножим его на два.
Запишем эллипс, описываемый исходным уравнением, в параметрическом виде. Параметризация эллипса в новых координатах обычна: \[ \left\{ \begin{array}{l} x'=\sqrt{2}a\cos t,\\ y'=\sqrt{\frac{2}{3}}a\sin t. \end{array}\right. \] Старые координаты можно вычислить через новые, подставив те, вместе с углолм $\alpha=\frac{\pi}{4}$, в (\ref{perehod}) \[ \left\{ \begin{array}{l} x=x'\cos\alpha-y'\sin\alpha=\sqrt{2}a\cos t\frac{1}{\sqrt{2}}-\sqrt{\frac{2}{3}}a\sin t\frac{1}{\sqrt{2}}=a\cos t-\frac{1}{\sqrt{3}}a\sin t,\\ y=x'\sin\alpha+y'\cos\alpha=\sqrt{2}a\cos t\frac{1}{\sqrt{2}}+\sqrt{\frac{2}{3}}a\sin t\frac{1}{\sqrt{2}}=a\cos t+\frac{1}{\sqrt{3}}a\sin t. \end{array}\right. \] Найдём значения параметра \(t\) для важных точек графика. В точках пересечения с $Ox$ $y=0$, а значит, \[ a\cos t+\frac{1}{\sqrt{3}}a\sin t=0, \] \[ \frac{\sqrt{3}}{2}\cos t+\frac{1}{2}\sin t=0, \] \[ \sin\frac{\pi}{3}\cos t+\cos\frac{\pi}{3}\sin t=0, \] \[ \sin\left(\frac{\pi}{3}+t\right)=0, \] \[ \frac{\pi}{3}+t=\pi n,\;n\in\mathbb{Z}. \] В пределах одного оборота таких решения два: \[ t_{1}=-\frac{\pi}{3},\qquad t_{2}=\frac{2\pi}{3}. \] При этом \[ x_{1}=a\cos\left(-\frac{\pi}{3}\right)-\frac{1}{\sqrt{3}}a\sin\left(-\frac{\pi}{3}\right)=a, \] \[ x_{2}=a\cos\frac{2\pi}{3}-\frac{1}{\sqrt{3}}a\sin\frac{2\pi}{3}=a\cos\left(\pi-\frac{\pi}{3}\right)-\frac{1}{\sqrt{3}}a\sin\left(\pi-\frac{\pi}{3}\right)=-\frac{1}{2}a-\frac{1}{\sqrt{3}}\frac{\sqrt{3}}{2}a=-a. \] Назовём эти точки соответственно точками $A$ и $C$.
В точках пересечения с $Oy$ $x=0$, \[ a\cos t-\frac{1}{\sqrt{3}}a\sin t=0, \] \[ \sin\left(\frac{\pi}{3}-t\right)=0, \] \[ \frac{\pi}{3}-t=\pi n,\;n\in\mathbb{Z}. \] В пределах одного оборота таких решения два: \[ t_{1}=\frac{\pi}{3},\qquad t_{2}=-\frac{2\pi}{3}. \] При этом \[ y_{1}=a\cos\frac{\pi}{3}+\frac{1}{\sqrt{3}}a\sin\frac{\pi}{3}=\frac{1}{2}a+\frac{1}{\sqrt{3}}a\frac{\sqrt{3}}{2}=a, \] \[ y_{2}=a\cos\left(-\frac{2\pi}{3}\right)+\frac{1}{\sqrt{3}}a\sin\left(-\frac{2\pi}{3}\right)=a\cos\left(\frac{\pi}{3}-\pi\right)+\frac{1}{\sqrt{3}}a\sin\left(\frac{\pi}{3}-\pi\right)=-a\cos\left(\frac{\pi}{3}\right)-\frac{1}{\sqrt{3}}a\sin\frac{\pi}{3}=-\frac{1}{2}a-\frac{1}{\sqrt{3}}a\frac{\sqrt{3}}{2}=-a. \] Точку с координатами $\left(0,a\right)$ назовём точкой $D$.
Заметим также, что $x$ зависит от $t$ немонотонно. Найдём точку, в которой $x$ максимально, а значит, \[ \frac{d}{dt}x=\frac{d}{dt}\left(\cos t-\frac{1}{\sqrt{3}}\sin t\right)=-\sin t-\frac{1}{\sqrt{3}}\cos t=0, \] \[ \frac{\sqrt{3}}{2}\sin t+\frac{1}{2}\cos t=0, \] \[ \cos\frac{\pi}{6}\sin t+\sin\frac{\pi}{6}\cos t=0, \] \[ \sin\left(t+\frac{\pi}{6}\right)=0, \] \[ t+\frac{\pi}{6}=\pi n, \] \[ t=-\frac{\pi}{6}+\pi n,\;n\in\mathbb{Z}. \] Между точками $A$ и $D$, то есть при $-\frac{\pi}{3}\leqslant t\leqslant\frac{\pi}{3}$, такая точка одна: $t=-\frac{\pi}{6}$. Назовём эту точку $B$, её координаты будут $\left(\frac{2a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)$.
Чтобы получить объём тела вращения, образованного вращением дуги $AD$ (рис. 3), понадобится вычесть из объёма тела, образованного вращением $BD$ (рис. 4), объём тела, образованного вращением дуги $AB$ (рис. 5).
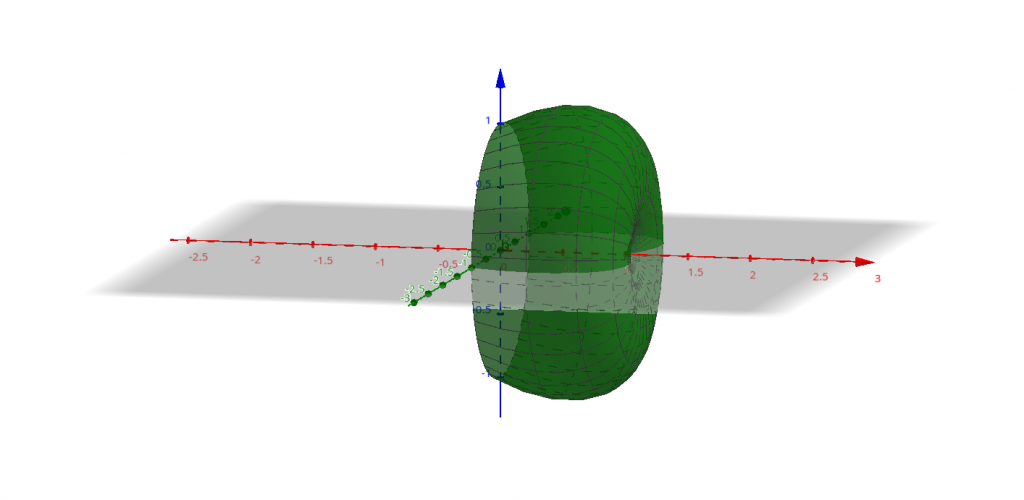
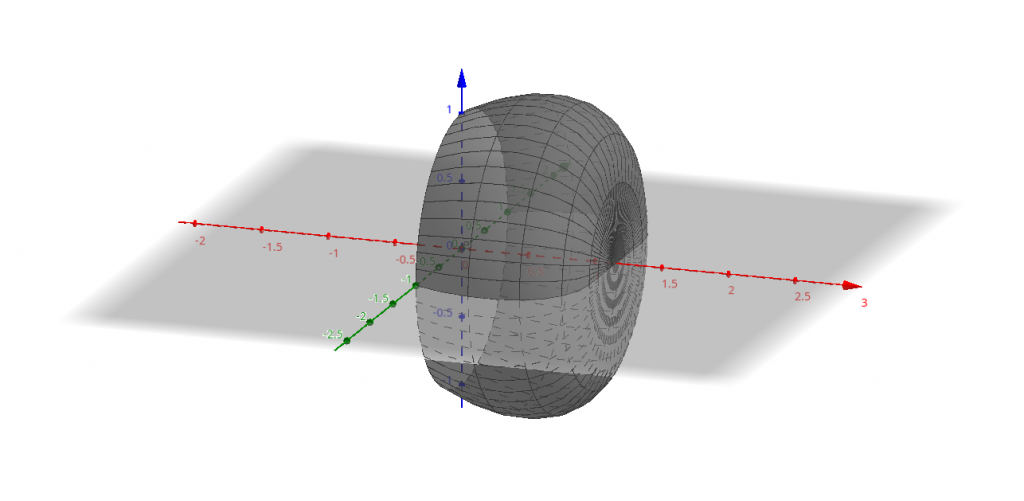

Обе этих дуги описываются одинаковыми функциями $x\left(t\right)$ и $y\left(t\right)$ , но при разных диапазонах $t$: $AB$ - при $-\frac{\pi}{3}\leqslant t\leqslant-\frac{\pi}{6}$, а $BD$ - при $-\frac{\pi}{6}\leqslant t\leqslant\frac{\pi}{3}$, поэтому имеет смысл записать общую формулу для объёма такой фигуры: \[ V=\pi\intop_{x_{1}}^{x_{2}}y^{2}dx=\pi\intop_{t_{1}}^{t_{2}}y^{2}\frac{dx}{dt}dt=\pi\intop_{t_{1}}^{t_{2}}\left(a\cos t+\frac{1}{\sqrt{3}}a\sin t\right)^{2}\frac{d}{dt}\left(a\cos t-\frac{1}{\sqrt{3}}a\sin t\right)dt= \] \[ =-\pi a^{3}\intop_{t_{1}}^{t_{2}}\left(\cos^{2}t+\frac{2}{\sqrt{3}}\cos t\sin t+\frac{1}{3}\sin^{2}t\right)\left(\sin t+\frac{1}{\sqrt{3}}\cos t\right)dt= \] \[ =-\pi a^{3}\intop_{t_{1}}^{t_{2}}\left(\cos^{2}t\sin t+\frac{2}{\sqrt{3}}\cos t\sin^{2}t+\frac{1}{3}\sin^{3}t+\frac{1}{\sqrt{3}}\cos^{3}t+\frac{2}{3}\cos^{2}t\sin t+\frac{1}{3\sqrt{3}}\cos t\sin^{2}t\right)dt= \] \[ =-\pi a^{3}\intop_{t_{1}}^{t_{2}}\left(\cos^{2}t\sin t+\frac{2}{\sqrt{3}}\cos t\sin^{2}t+\frac{1}{3}\left(1-\cos^{2}t\right)\sin t+\frac{1}{\sqrt{3}}\left(1-\sin^{2}t\right)\cos t+\frac{2}{3}\cos^{2}t\sin t+\frac{1}{3\sqrt{3}}\cos t\sin^{2}t\right)dt= \] \[ =-\pi a^{3}\left.\left(-\frac{\cos^{3}t}{3}+\frac{2}{\sqrt{3}}\frac{\sin^{3}t}{3}-\frac{1}{3}\left(\cos t-\frac{\cos^{3}t}{3}\right)+\frac{1}{\sqrt{3}}\left(\sin t-\frac{\sin^{3}t}{3}\right)-\frac{2}{3}\frac{\cos^{3}t}{3}+\frac{1}{3\sqrt{3}}\frac{\sin^{3}t}{3}\right)\right|_{t_{1}}^{t_{2}}= \] \[ =-\pi a^{3}\left.\left(-\frac{\cos^{3}t}{3}+\frac{2}{3\sqrt{3}}\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{9}\cos^{3}t+\frac{1}{\sqrt{3}}\sin t-\frac{1}{3\sqrt{3}}\sin^{3}t-\frac{2}{9}\cos^{3}t+\frac{1}{9\sqrt{3}}\sin^{3}t\right)\right|_{t_{1}}^{t_{2}}= \] \[ =-\pi a^{3}\left.\left[\left(-\frac{1}{3}+\frac{1}{9}-\frac{2}{9}\right)\cos^{3}t+\left(\frac{2}{3\sqrt{3}}-\frac{1}{3\sqrt{3}}+\frac{1}{9\sqrt{3}}\right)\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{\sqrt{3}}\sin t\right]\right|_{t_{1}}^{t_{2}}= \] \[ =-\pi a^{3}\left.\left(-\frac{4}{9}\cos^{3}t+\frac{4}{9\sqrt{3}}\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{\sqrt{3}}\sin t\right)\right|_{t_{1}}^{t_{2}}. \]
Начнём с $V_{BD}$. Замечу, что для возрастания $x$ придётся в качестве нижнего предела интегрирования подставить значение $t$ для точки $D$, а в качестве верхнего - для точки $B$. \[ V_{BD}=\pi\intop_{\pi/3}^{-\pi/6}y^{2}\frac{dx}{dt}dt=-\pi a^{3}\left.\left(-\frac{4}{9}\cos^{3}t+\frac{4}{9\sqrt{3}}\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{\sqrt{3}}\sin t\right)\right|_{\pi/3}^{-\pi/6}= \] Теперь - объём вычитаемого тела $V_{AB}$: \[ V_{AB}=\pi\intop_{-\pi/3}^{-\pi/6}y^{2}\frac{dx}{dt}dt. \] Тогда (считаю не спеша, внося небольшие изменения за раз, так что следите) \[ V_{AD}=V_{BD}-V_{AB}=\pi\intop_{\pi/3}^{-\pi/6}y^{2}\frac{dx}{dt}dt-\pi\intop_{-\pi/3}^{-\pi/6}y^{2}\frac{dx}{dt}dt=\pi\intop_{\pi/3}^{-\pi/3}y^{2}\frac{dx}{dt}dt= \] \[ =-\pi a^{3}\left.\left(-\frac{4}{9}\cos^{3}t+\frac{4}{9\sqrt{3}}\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{\sqrt{3}}\sin t\right)\right|_{\pi/3}^{-\pi/3}=\pi a^{3}\left.\left(-\frac{4}{9}\cos^{3}t+\frac{4}{9\sqrt{3}}\sin^{3}t-\frac{1}{3}\cos t+\frac{1}{\sqrt{3}}\sin t\right)\right|_{-\pi/3}^{\pi/3}= \] \[ =\pi a^{3}\left[\left(-\frac{4}{9}\cos^{3}\frac{\pi}{3}+\frac{4}{9\sqrt{3}}\sin^{3}\frac{\pi}{3}-\frac{1}{3}\cos\frac{\pi}{3}+\frac{1}{\sqrt{3}}\sin\frac{\pi}{3}\right)-\left(-\frac{4}{9}\cos^{3}\left(-\frac{\pi}{3}\right)+\frac{4}{9\sqrt{3}}\sin^{3}\left(-\frac{\pi}{3}\right)-\frac{1}{3}\cos\left(-\frac{\pi}{3}\right)+\frac{1}{\sqrt{3}}\sin\left(-\frac{\pi}{3}\right)\right)\right]= \] \[ =\pi a^{3}\left[-\frac{4}{9}\cos^{3}\frac{\pi}{3}+\frac{4}{9\sqrt{3}}\sin^{3}\frac{\pi}{3}-\frac{1}{3}\cos\frac{\pi}{3}+\frac{1}{\sqrt{3}}\sin\frac{\pi}{3}+\frac{4}{9}\cos^{3}\frac{\pi}{3}+\frac{4}{9\sqrt{3}}\sin^{3}\frac{\pi}{3}+\frac{1}{3}\cos\frac{\pi}{3}+\frac{1}{\sqrt{3}}\sin\frac{\pi}{3}\right]= \] \[ =\pi a^{3}\left[\frac{8}{9\sqrt{3}}\sin^{3}\frac{\pi}{3}+\frac{2}{\sqrt{3}}\sin\frac{\pi}{3}\right]=\pi a^{3}\left[\frac{8}{9\sqrt{3}}\left(\frac{\sqrt{3}}{2}\right)^{3}+\frac{2}{\sqrt{3}}\frac{\sqrt{3}}{2}\right]=\pi a^{3}\left[\frac{8}{9\sqrt{3}}\frac{3\sqrt{3}}{8}+1\right]=\frac{4}{3}\pi a^{3}. \] Полный объём, напомню, равен удвоенному $V_{AD}$: \[ V=2V_{AD}=\frac{8}{3}\pi a^{3}, \] что и было в ответе.
К решению, для интересующихся, прилагаю архив с файлами геометрических построений в геогебре, с которых были сняты иллюстрации в ээтом посте, и расчётов в максиме (с оболочкой wxMaxima). Учтите, что в максиме я считал несколько иначе, чем в этом посте.
