Задача на объём — в помощь тем, кто разбирается с телами вращения.
Найти объём тела, полученного при вращении кривой x2−xy+y2=a2 вокруг оси Ox.
Нередко бывает, что кратко формулируемая задача имеет долгое и тяжёлое решение и доставляет массу проблем на ровном месте. В аудитории такие задачи решать некогда, дома их, как правило, не осиливают, а знать о них надо. И вот, появился хороший повод такие задачи поразбирать.
Заметим, что уравнение в нашем номере, вроде бы короткое и простое, не только не является каноническим уравнением какой-либо кривой второго порядка, но и не приводится к таковому без поворотов.
При повороте координатных осей на угол α координаты x′ и y′ в новой системе связаны с координатами x и y в старой по такому закону: {x=x′cosα−y′sinα,y=x′sinα+y′cosα. Подставив эти замены в уравнение (1) и собрав слагаемые с одинаковыми степенями координат, получим (1−sinαcosα)x′2+(2sin2α−1)x′y′+(1+sinαcosα)y′2=a2. Из этого уравнения исчезнет x′y′, если 2sin2α−1=0, sinα=1√2,α=π4. Полученное решение для α, конечно, не единственное, но нас устроит любое из решений. Подставим полученное α в (3) (1−12)x′2+(1+12)y′2=a2, x′22+3y′22=a2. Легко заметить, что в координатах x′ и y′ последнее уравнение описывает эллипс с полуосями √2 и √23, изображённый на рис. 1 (синяя линия).
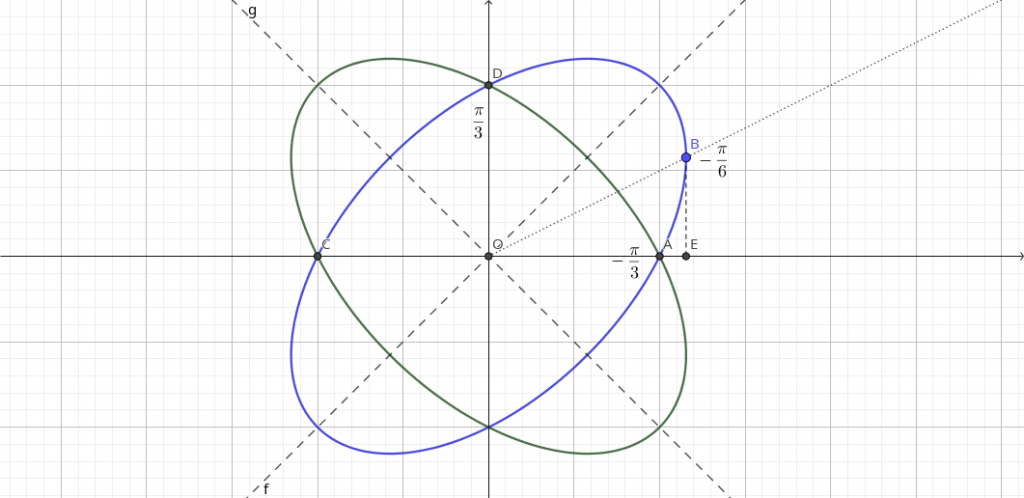
Если этот эллипс вращать вокруг оси Ox, он опишет фигуру на рис. 2, ещё раз пересёкшись с плоскостью xy (по серой линии на рис. 1) после полуоборота.
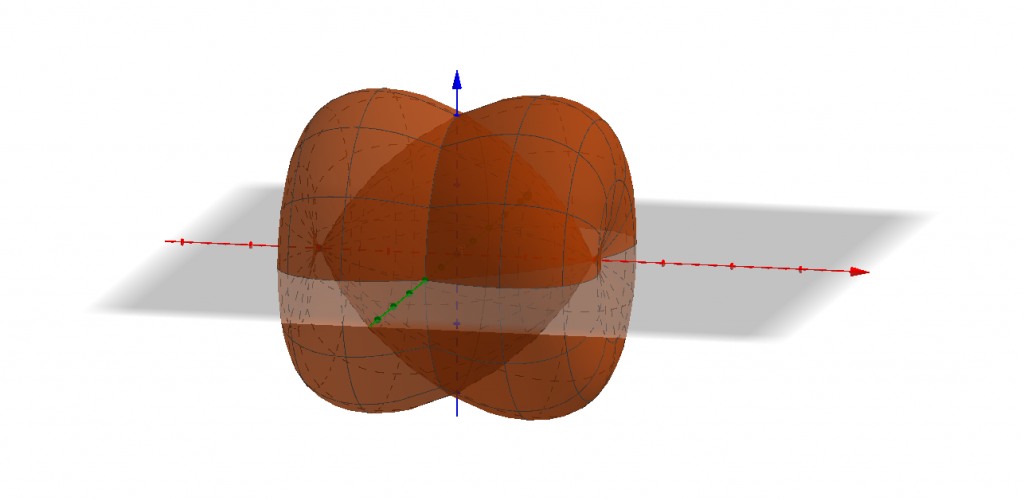
Так как серая линия получена поворотом вокруг оси Ox, её уравнение можно получить заменой в исходном уравнении y на −y: x2+xy+y2=a2 Однако то же самое получится, если заменить x на −x. Тело вращения исходной кривой получится таким же, как если бы мы вращали объединённую сине-серую кривую на рис. 1. При этом последняя симметрична относительно оси Oy (каждой точке синей кривой справа соответствует точка серой кривой слева, и наоборот), следовательно, тело вращения симметрично относительно плоскости yz. Поэтому для нахождения его объёма мы найдём объём правой части и умножим его на два.
Запишем эллипс, описываемый исходным уравнением, в параметрическом виде. Параметризация эллипса в новых координатах обычна: {x′=√2acost,y′=√23asint. Старые координаты можно вычислить через новые, подставив те, вместе с углолм α=π4, в (2) {x=x′cosα−y′sinα=√2acost1√2−√23asint1√2=acost−1√3asint,y=x′sinα+y′cosα=√2acost1√2+√23asint1√2=acost+1√3asint. Найдём значения параметра t для важных точек графика. В точках пересечения с Ox y=0, а значит, acost+1√3asint=0, √32cost+12sint=0, sinπ3cost+cosπ3sint=0, sin(π3+t)=0, π3+t=πn,n∈Z. В пределах одного оборота таких решения два: t1=−π3,t2=2π3. При этом x1=acos(−π3)−1√3asin(−π3)=a, x2=acos2π3−1√3asin2π3=acos(π−π3)−1√3asin(π−π3)=−12a−1√3√32a=−a. Назовём эти точки соответственно точками A и C.
В точках пересечения с Oy x=0, acost−1√3asint=0, sin(π3−t)=0, π3−t=πn,n∈Z. В пределах одного оборота таких решения два: t1=π3,t2=−2π3. При этом y1=acosπ3+1√3asinπ3=12a+1√3a√32=a, y2=acos(−2π3)+1√3asin(−2π3)=acos(π3−π)+1√3asin(π3−π)=−acos(π3)−1√3asinπ3=−12a−1√3a√32=−a. Точку с координатами (0,a) назовём точкой D.
Заметим также, что x зависит от t немонотонно. Найдём точку, в которой x максимально, а значит, ddtx=ddt(cost−1√3sint)=−sint−1√3cost=0, √32sint+12cost=0, cosπ6sint+sinπ6cost=0, sin(t+π6)=0, t+π6=πn, t=−π6+πn,n∈Z. Между точками A и D, то есть при −π3⩽t⩽π3, такая точка одна: t=−π6. Назовём эту точку B, её координаты будут (2a√3;a√3).
Чтобы получить объём тела вращения, образованного вращением дуги AD (рис. 3), понадобится вычесть из объёма тела, образованного вращением BD (рис. 4), объём тела, образованного вращением дуги AB (рис. 5).
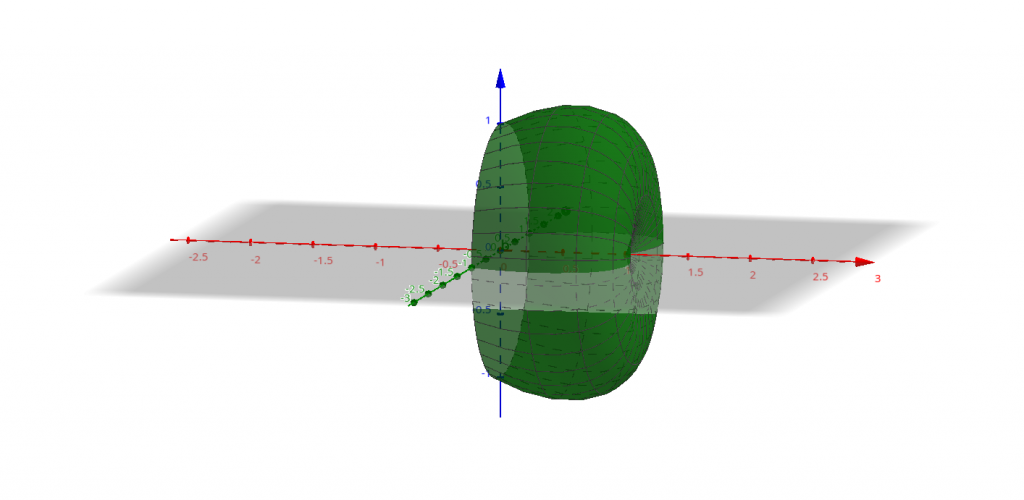
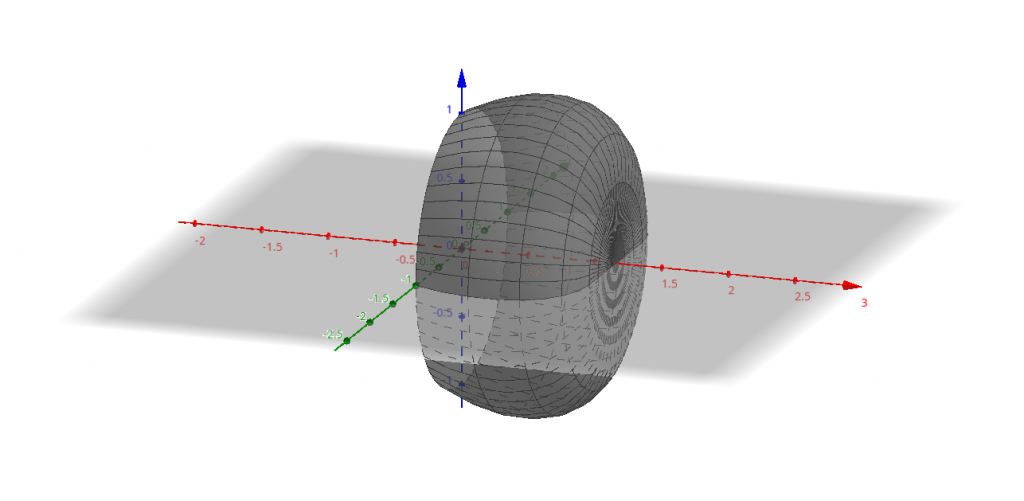

Обе этих дуги описываются одинаковыми функциями x(t) и y(t) , но при разных диапазонах t: AB - при −π3⩽t⩽−π6, а BD - при −π6⩽t⩽π3, поэтому имеет смысл записать общую формулу для объёма такой фигуры: V=πx2∫x1y2dx=πt2∫t1y2dxdtdt=πt2∫t1(acost+1√3asint)2ddt(acost−1√3asint)dt= =−πa3t2∫t1(cos2t+2√3costsint+13sin2t)(sint+1√3cost)dt= =−πa3t2∫t1(cos2tsint+2√3costsin2t+13sin3t+1√3cos3t+23cos2tsint+13√3costsin2t)dt= =−πa3t2∫t1(cos2tsint+2√3costsin2t+13(1−cos2t)sint+1√3(1−sin2t)cost+23cos2tsint+13√3costsin2t)dt= =−πa3(−cos3t3+2√3sin3t3−13(cost−cos3t3)+1√3(sint−sin3t3)−23cos3t3+13√3sin3t3)|t2t1= =−πa3(−cos3t3+23√3sin3t−13cost+19cos3t+1√3sint−13√3sin3t−29cos3t+19√3sin3t)|t2t1= =−πa3[(−13+19−29)cos3t+(23√3−13√3+19√3)sin3t−13cost+1√3sint]|t2t1= =−πa3(−49cos3t+49√3sin3t−13cost+1√3sint)|t2t1.
Начнём с VBD. Замечу, что для возрастания x придётся в качестве нижнего предела интегрирования подставить значение t для точки D, а в качестве верхнего - для точки B. VBD=π−π/6∫π/3y2dxdtdt=−πa3(−49cos3t+49√3sin3t−13cost+1√3sint)|−π/6π/3= Теперь - объём вычитаемого тела VAB: VAB=π−π/6∫−π/3y2dxdtdt. Тогда (считаю не спеша, внося небольшие изменения за раз, так что следите) VAD=VBD−VAB=π−π/6∫π/3y2dxdtdt−π−π/6∫−π/3y2dxdtdt=π−π/3∫π/3y2dxdtdt= =−πa3(−49cos3t+49√3sin3t−13cost+1√3sint)|−π/3π/3=πa3(−49cos3t+49√3sin3t−13cost+1√3sint)|π/3−π/3= =πa3[(−49cos3π3+49√3sin3π3−13cosπ3+1√3sinπ3)−(−49cos3(−π3)+49√3sin3(−π3)−13cos(−π3)+1√3sin(−π3))]= =πa3[−49cos3π3+49√3sin3π3−13cosπ3+1√3sinπ3+49cos3π3+49√3sin3π3+13cosπ3+1√3sinπ3]= =πa3[89√3sin3π3+2√3sinπ3]=πa3[89√3(√32)3+2√3√32]=πa3[89√33√38+1]=43πa3. Полный объём, напомню, равен удвоенному VAD: V=2VAD=83πa3, что и было в ответе.
К решению, для интересующихся, прилагаю архив с файлами геометрических построений в геогебре, с которых были сняты иллюстрации в ээтом посте, и расчётов в максиме (с оболочкой wxMaxima). Учтите, что в максиме я считал несколько иначе, чем в этом посте.
