Перейти к полярным координатам и расставить пределы интегрирования в том и в другом порядке в интеграле:
1∫0dx√1−x2∫1−xdyf(x,y)
Якобиан перехода от декартовых координат к полярным, как известно с прошлого занятия, равен r.
Вначале поставим снаружи интеграл по dφ:
1∫0dx√1−x2∫1−xdyf(x,y)=∫dφ∫drf(x,y)r.
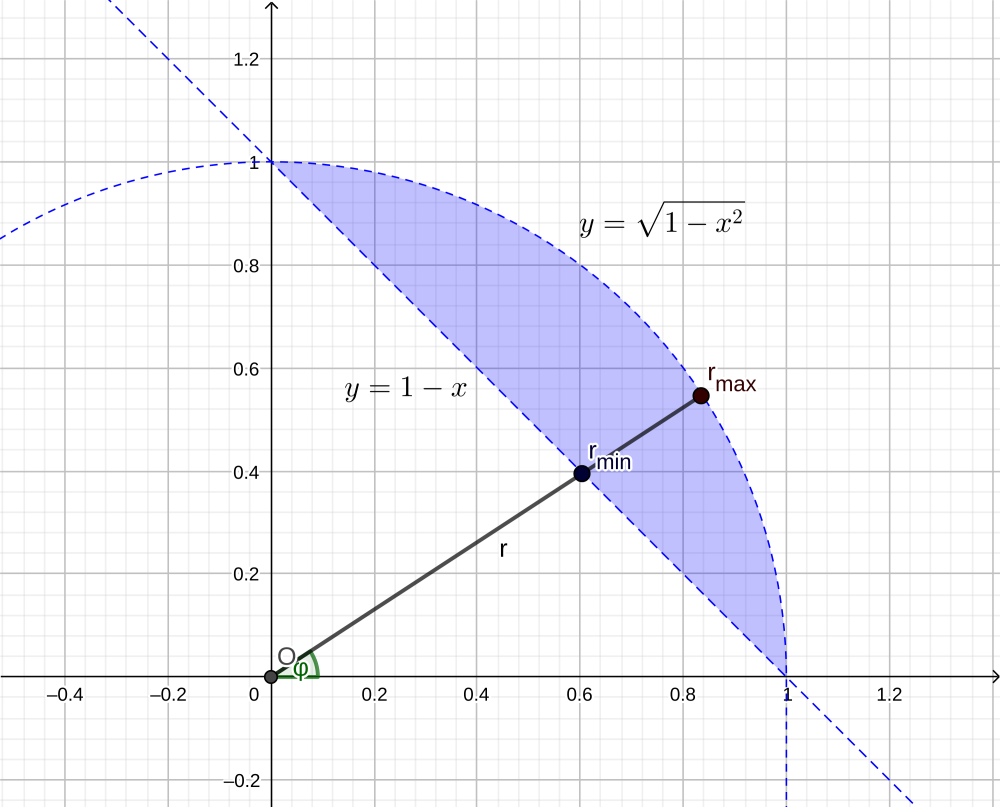
Осталось в последнем интеграле расставить пределы интегрирования. (см. рис. 1) Для координаты φ для этого нужно искать наименьшее и наибольшее значения, которые она принимает в точках (1;0), где φ=0, и (0;1), где φ=π2.
Координата r, так как имеет смысл расстояния от начала координат, принимает наибольшие значения на самых дальних точках, т.е. точках дуги единичной окружности, где r=1. Наименьшие же значения она принимает в точках хорды, где
y=1−x,
причём для каждого φ это значение своё:
rsinφ=1−rcosφ,
r(sinφ+cosφ)=1,
r=1sinφ+cosφ.
Итак,
1∫0dx√1−x2∫1−xdyf(x,y)=π2∫0dφ1∫1sinφ+cosφdrf(x,y)r.
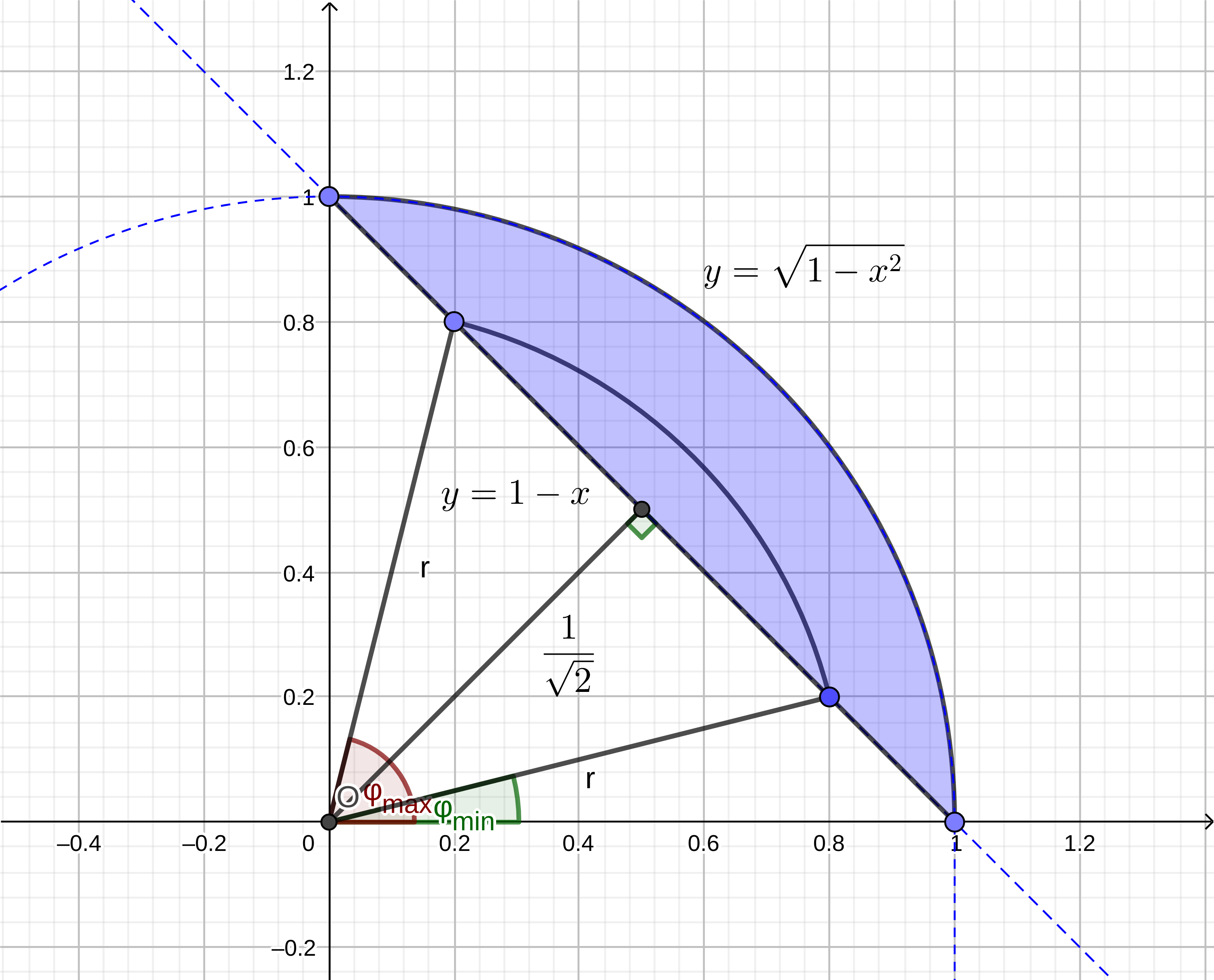
Если же теперь снаружи поставить интеграл по dr, то придётся искать наименьшее и наибольшее значения r на всей области интегрирования. Наибольшее, как мы уже знаем, равно 1, а наименьшее достигается в точке, в которую падает перпендикуляр к хорде, ограничивающей область интегрирования снизу (см. рис. 2). Нетрудно видеть, что оно равно 1√2.
Множество точек с одинаковым r образует дугу радиуса r, которая, проходя через нашу область интегрирования, пересекает хорду y=1−x в двух местах; в левой нижней из этих точек достигается наименьшее значение φ при данном r, в правой верхней — наибольшее. Находятся они, как и в предыдущем случае, из уравнения хорды в полярных координатах, но теперь мы решаем его относительно φ:
r(sinφ+cosφ)=1,
sinφ+cosφ=cos(π2−φ)+cosφ=2cosπ4cos(π4−φ)=√2cos(φ−π4),
√2cos(φ−π4)=1r,
φ−π4=±arccos1√2r,
φ=π4±arccos1√2r,
φmin=π4−arccos1√2r,φmax=π4+arccos1√2r;
тогда
1∫0dx√1−x2∫1−xdyf(x,y)=1∫1/√2drπ4+arccos1√2r∫π4−arccos1√2rdφf(x,y)r.
