Переходя к полярным координатам, заменить двойной интеграл \[ \iint\limits _{x^{2}+y^{2}\leqslant x}f\left(\frac{y}{x}\right)dx \] однократным
Вначале изобразим фигуру, заданную неравенством, на плоскости. Для этого (смотрите внимательно, тов. Батталов) перенесём $x$ в левую часть и выделим полный квадрат \[ x^{2}+y^{2}\leqslant x \] \[ x^{2}-2x\frac{1}{2}+y^{2}\leqslant0 \] \[ x^{2}-2x\frac{1}{2}+\frac{1}{4}+y^{2}\leqslant\frac{1}{4} \] \[ \left(x-\frac{1}{2}\right)^{2}+y^{2}\leqslant\left(\frac{1}{2}\right)^{2} \]
Полученное будет кругом с центром в точке $\left(\frac{1}{2};0\right)$ и радиусом $\frac{1}{2}$.
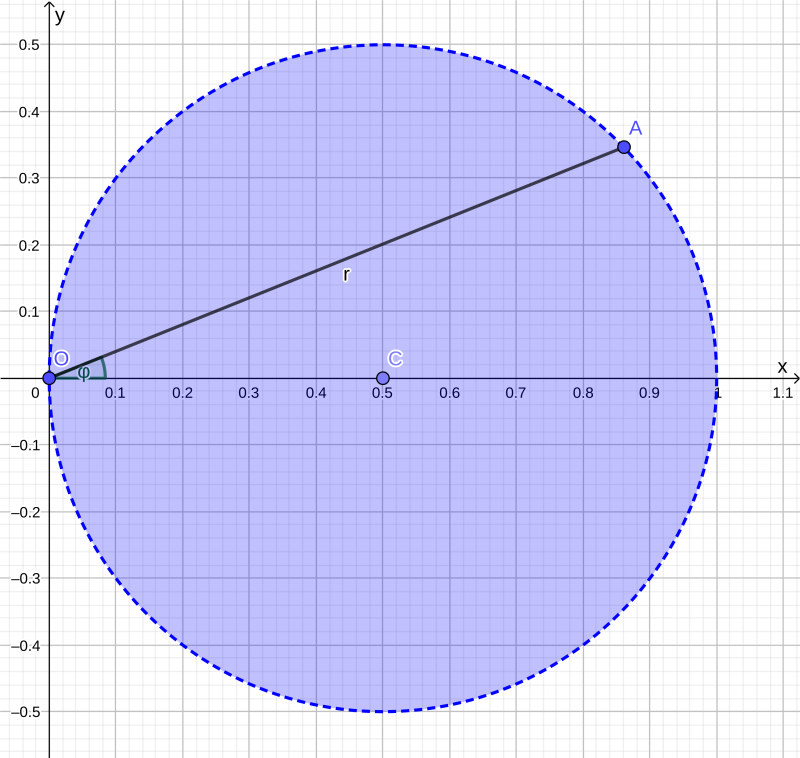
Переведём подынтегральное выражение в полярные кординаты: \[ \frac{y}{x}=\frac{r\sin\varphi}{r\cos\varphi}=\mathrm{tg}\,\varphi. \] Туда же переведём неравенство, задающее круг: \[ r^{2}\cos^{2}\varphi+r^{2}\sin^{2}\varphi\leqslant r\cos\varphi, \] \[ r\leqslant\cos\varphi. \] Далее, \[ r\geqslant0,\qquad\Rightarrow\qquad\cos\varphi\geqslant0,\qquad\Rightarrow\qquad-\frac{\pi}{2}\leqslant\varphi\leqslant\frac{\pi}{2}, \] в итоге \[ \iint\limits _{x^{2}+y^{2}\leqslant x}f\left(\frac{y}{x}\right)dx=\int\limits _{-\pi/2}^{\pi/2}d\varphi\int\limits _{0}^{\cos\varphi}drf\left(\mathrm{tg}\,\varphi\right)\cdot r= \] Внутренний интеграл из этого вложения можно, как оказывается, взять: \[ =\int\limits _{-\pi/2}^{\pi/2}d\varphi f\left(\mathrm{tg}\,\varphi\right)\int\limits _{0}^{\cos\varphi}rdr=\int\limits _{-\pi/2}^{\pi/2}d\varphi f\left(\mathrm{tg}\,\varphi\right)\frac{\cos^{2}\varphi}{2}=\frac{1}{2}\int\limits _{-\pi/2}^{\pi/2}f\left(\mathrm{tg}\,\varphi\right)\cos^{2}\varphi d\varphi= \] после чего интеграл оказывается, как и требовалось, однократным. Также можно, хотя от нас этого не требовали, заменить переменные, чтобы избавиться от тангенсов: $\mathrm{tg}\,\varphi=t$, \[ =\frac{1}{2}\int\limits _{-\pi/2}^{\pi/2}f\left(\mathrm{tg}\,\varphi\right)\cos^{4}\varphi\frac{d\varphi}{\cos^{2}\varphi}=\frac{1}{2}\int\limits _{-\pi/2}^{\pi/2}f\left(\mathrm{tg}\,\varphi\right)\left(\frac{1}{1+\mathrm{tg}^{2}\,\varphi}\right)^{2}\frac{d\varphi}{\cos^{2}\varphi}=\frac{1}{2}\int\limits _{-\infty}^{\infty}f\left(t\right)\left(\frac{1}{1+t^{2}}\right)^{2}dt=\frac{1}{2}\int\limits _{-\infty}^{\infty}\frac{f\left(t\right)dt}{\left(1+t^{2}\right)^{2}} \]
