В интеграле \[ \int\limits _{a}^{b}dx\int\limits _{\alpha x}^{\beta x}dyf\left(x,y\right),\qquad0 < a < b,\quad0 < \alpha < \beta, \] перейти к переменным: $u=x$, $v=y/x$ (обратно можно выразить $x=u$, $y=vx=uv$).
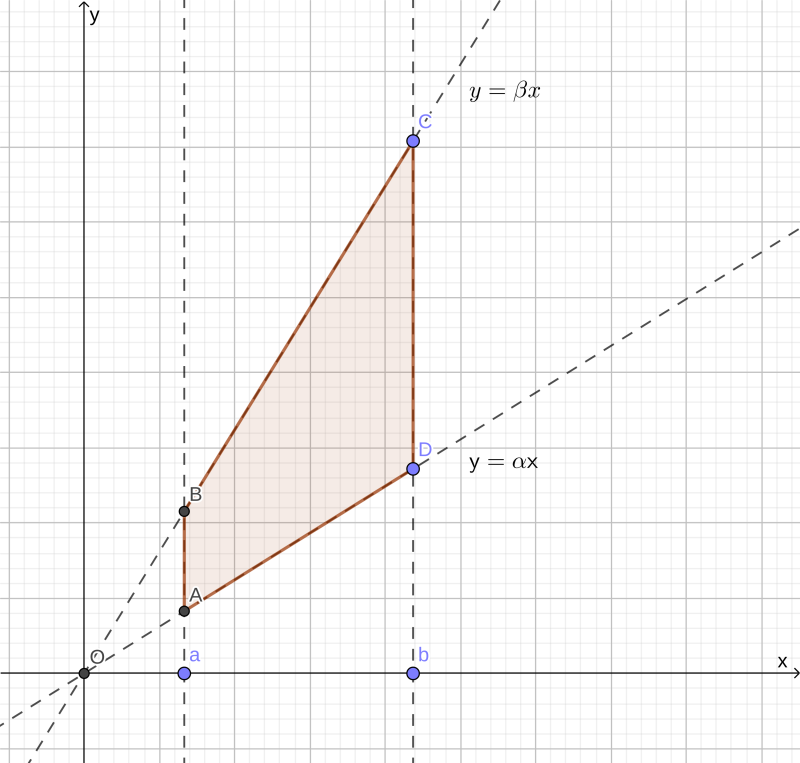
Сначала преобразуем область интегрирования. Из пределов интегрирования для $x$ получим \[ a\leqslant x\leqslant b,\quad x=u,\quad\Rightarrow\quad a\leqslant u\leqslant b. \] Заметим ещё, что \[ 0 < a\leqslant x\quad\Rightarrow\quad x > 0. \] Из пределов интегрирования для $y$ получим \[ \alpha x\leqslant y\leqslant\beta x\quad\Rightarrow\quad\alpha\leqslant\frac{y}{x}\leqslant\beta\quad\Rightarrow\quad\alpha\leqslant v\leqslant\beta, \] после чего область интегрирования становится прямоугольной: \[ \int\limits _{a}^{b}dx\int\limits _{\alpha x}^{\beta x}dyf\left(x,y\right)=\int\limits _{a}^{b}du\int\limits _{\alpha}^{\beta}dvf\left(u,uv\right)\left|J\right|. \] Замечу, что в отличие от однократных интегралов, где замены почти всегда делаются для упрощения или приведения к нужному виду подынтегрального выражения, в многократных это часто делают, чтобы аналогично «окирпичить» область интегрирования.
Вычислим теперь якобиан, который тоже понадобится в преобразованном интеграле: \[ J=\left|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{array}\right|=\left|\begin{array}{cc} 1 & v\\ 0 & u \end{array}\right|=u, \] \[ u=x > 0\quad\Rightarrow\quad\left|J\right|=\left|u\right|=u. \] Итак, \[ \int\limits _{a}^{b}dx\int\limits _{\alpha x}^{\beta x}dyf\left(x,y\right)=\int\limits _{a}^{b}du\int\limits _{\alpha}^{\beta}dvf\left(u,uv\right)\left|J\right|=\int\limits _{a}^{b}du\int\limits _{\alpha}^{\beta}dvf\left(u,uv\right)u. \]
