Произведя соответствующую замену переменных, свести двойной интеграл \[ \iint\limits _{\left|x\right|+\left|y\right|\leqslant1}f\left(x+y\right)dxdy \] к однократному.
В этом номере замена переменных и вовсе не дана, и её нужно подобрать самим. Отмечу, что предлагаемая мной замена -- не единственная годная, заменить можно было и по-другому. Вначале изобразим область интегрирования:
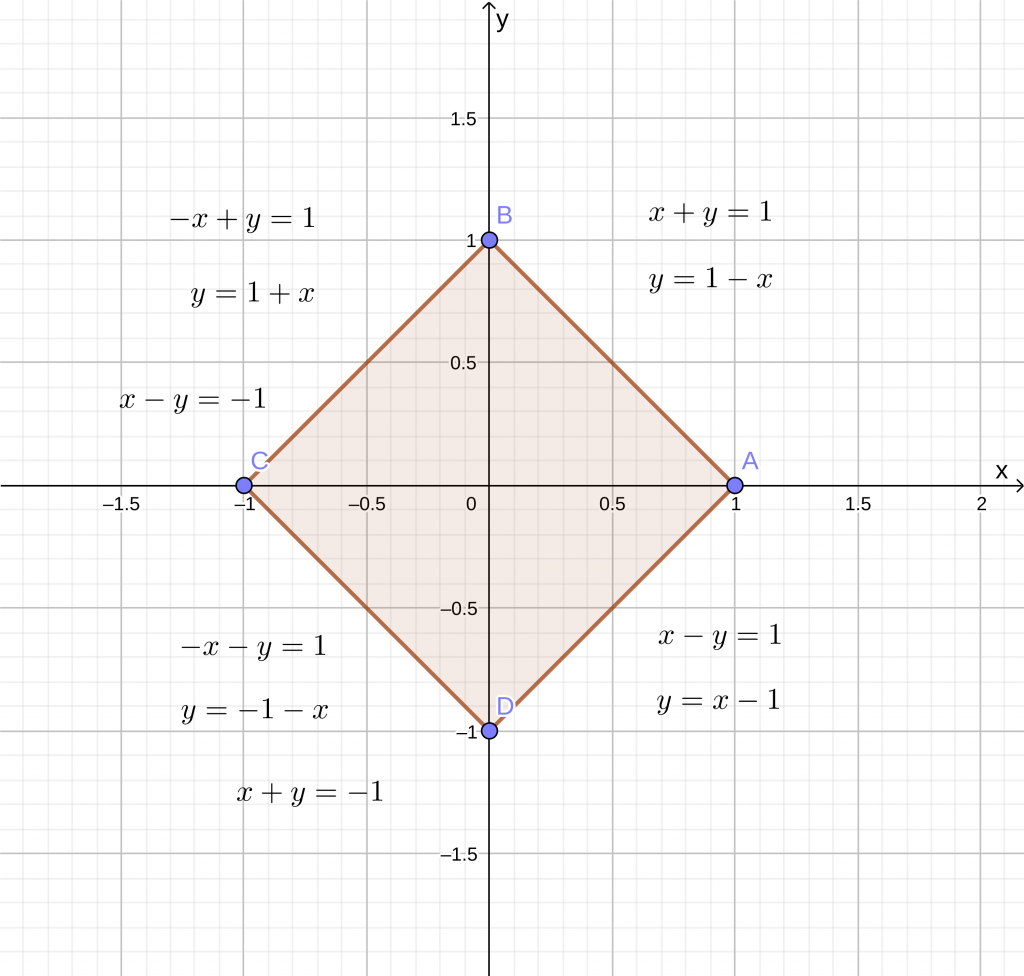
В каждой четверти модули в неравенстве, задающем область интегрирования, раскрываются по-своему, соответствующие вычисления приведены на чертеже. Заметим, что на гранях полученного квадрата, лежащих в первой и третьей четвертях, постоянно выражение $x+y$ (и равно $+1$ или $-1$), а на остальных двух -- $x-y$ (с теми же значениями). Поэтому заменим $x+y=u$, $x-y=v$. В новых координатах область интегрирования будет ограничена четырьмя кривыми, задаваемыми уравнениями $u=\pm1$ и $v=\pm1$:
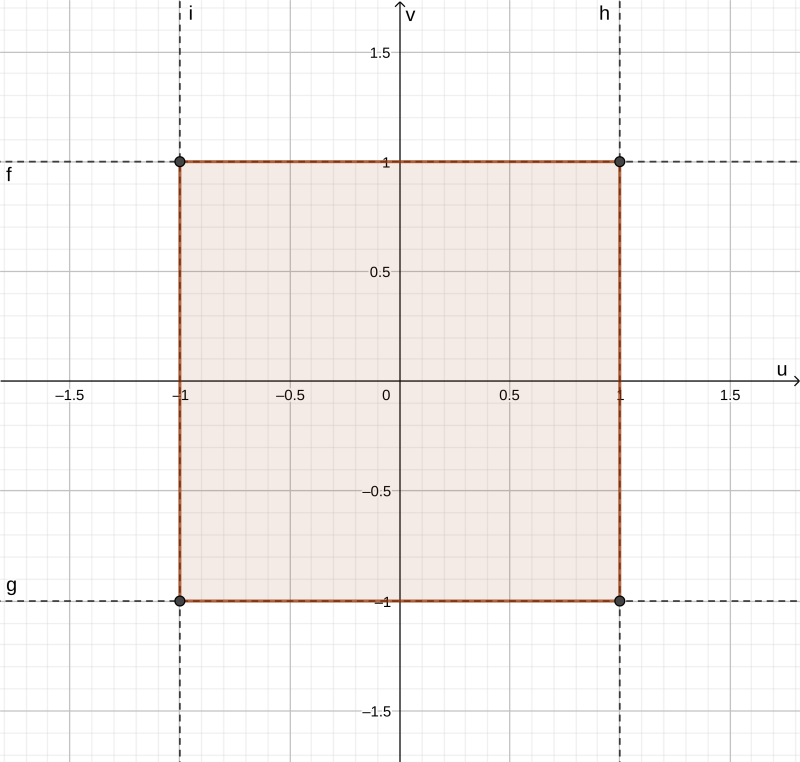
По этой области и будем интегрировать. Якобиан перехода вычисляется так:
\[
J^{-1}=\left|\begin{array}{cc}
\frac{\partial u}{\partial x} & \frac{\partial v}{\partial x}\\
\frac{\partial u}{\partial y} & \frac{\partial v}{\partial y}
\end{array}\right|=\left|\begin{array}{cr}
1 & 1\\
1 & -1
\end{array}\right|=-2,\qquad\left|J\right|=\left|\frac{1}{-2}\right|=\frac{1}{2}.
\]
Тогда
\[
\iint\limits _{\left|x\right|+\left|y\right|\leqslant1}f\left(x+y\right)dxdy=\int\limits _{-1}^{1}du\left(\int\limits _{-1}^{1}dvf\left(u\right)\cdot\frac{1}{2}\right)=
\]
затем вынося что не интегрируется и интегрируя что интегрируется, получим
\[
=\frac{1}{2}\int\limits _{-1}^{1}\left(f\left(u\right)du\int\limits _{-1}^{1}dv\right)=\frac{1}{2}\int\limits _{-1}^{1}\left(f\left(u\right)du2\right)=\int\limits _{-1}^{1}f\left(u\right)du.
\]
Это уже однократный интеграл, который и требовалось получить.
