Рассмотрим произведение:
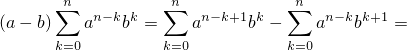
(во второй сумме заменяется 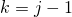 ):
):
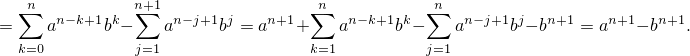
Итак,
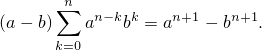
В частности, когда 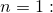
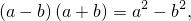
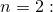
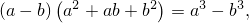
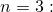
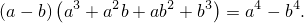
Теперь пусть 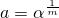 ;
; 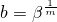 . Тогда
. Тогда
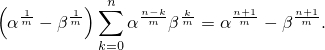
В частности, когда 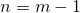 ,
,
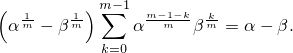
Так можно избавиться от разности корней любой степени.
Рассмотрим произведение:
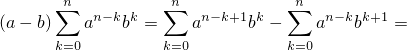
(во второй сумме заменяется 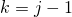 ):
):
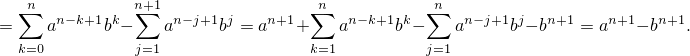
Итак,
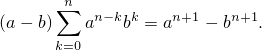
В частности, когда 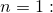
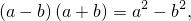
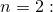
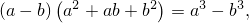
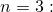
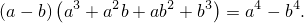
Теперь пусть 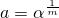 ;
; 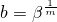 . Тогда
. Тогда
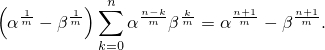
В частности, когда 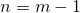 ,
,
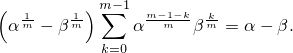
Так можно избавиться от разности корней любой степени.
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников