Уравнение №8:

Заметим, что тут
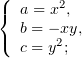
так как b2 − ac = 0, уравнение относится к параболическому типу. Уравнение
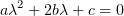
имеет один корень
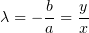
На переменную s заменим функцию, которую получим, как всегда, из уравнения
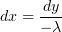
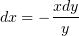
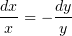
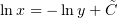
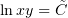
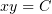
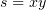
В качестве переменной t, в силу причин, объяснённых (здесь here), можно
выбрать любую независимую от s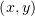 функцию. Для простоты мы выберем
t = x. Проверим якобиан:
функцию. Для простоты мы выберем
t = x. Проверим якобиан:
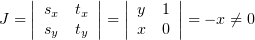
везде, кроме оси y.
Произведя замену переменных, мы получим уравнение
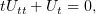
т.е.
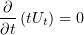
или
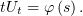
Отсюда
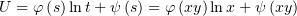
(если замену взять иначе, s = y, t = xy - получится ответ как в методичке).
Просили также показать №9, но там показывать особо нечего. С учётом условий задачи, гласящих что x > 0 и y > 0, b2 − ac = xy > 0 и уравнение относится к самому обычному гиперболическому типу.
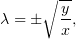
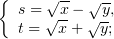
и после такого преобразования уравнение сводится к виду
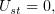
а значит
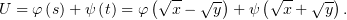
Даишев и Никитин функции преобразования выбрали наоборот.
