Просили выложить решения к номерам 11, 12 и 13. Они решаются общим
методом: заменяется искомая функция по формуле 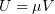 , где
, где 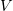 будет
новой искомой функцией, а
будет
новой искомой функцией, а 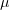 ищется из соображений максимального удобства.
Мы будем подбирать
ищется из соображений максимального удобства.
Мы будем подбирать 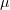 так, чтобы функция
так, чтобы функция 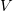 входила в уравнение только в
виде вторых производных.
входила в уравнение только в
виде вторых производных.
1 №11
 | (1) |
Если раскрыть производную в левой части,

Заменим  . Если
. Если  будет зависеть от
будет зависеть от  , то производные
, то производные  по
по  в
правой части не удастся скомпенсировать ничем, так что будем считать
в
правой части не удастся скомпенсировать ничем, так что будем считать
 . После замены
. После замены


 | (2) |
Будем искать такое  , чтобы в этом уравнении
, чтобы в этом уравнении  были только во вторых
производных. Для этого необходимо, чтобы
были только во вторых
производных. Для этого необходимо, чтобы
 | (3) |
Из первого

Подставим во второе

выполняется.
С учётом вполнения (3), после замены

уравнение (2) превратится в

т.е.

Дальше оно решается как обычное гиперболическое с постоянными
коэффициентами, через найденное  находится
находится  .
.
2 №12

 ,
,  Подставив и продифференцировав, получим
Подставив и продифференцировав, получим

 | (4) |
и в этом уравнении обнулятся коэффициенты при первых и нулевых
производных  при выполнении таких условий:
при выполнении таких условий:
 | (5) |
Из первого получим, что

и подставим во второе, чтобы получить  :
:







и третье уравнение из (5) даст

Мы нашли такое  , которое удовлетворяет всем условиям (5). Значит,
выполнив замену
, которое удовлетворяет всем условиям (5). Значит,
выполнив замену

мы сведём уравнение (4) к уравнению

или

Дальнейшее понятно.
№ 13 делается аналогично 12му, причём находится, что

