Найти экстремумы функции
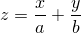 | (1) |
при условии
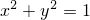 | (2) |
Для нахождения стационарных точек составим функцию Лагранжа
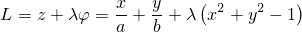
и приравняем её дифференциал к нулю
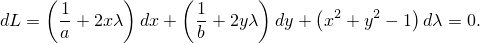
Отсюда получим систему
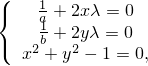
которую далее будем решать:
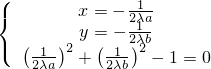
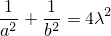
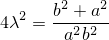
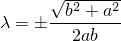
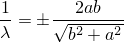
Получаем две точки:
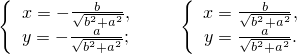
Для выяснения характера найденных стационарных точек нам потребуется
второй дифференциал  при условии (2). Из последнего, найдя дифференциал
от обеих частей, мы получим, что
при условии (2). Из последнего, найдя дифференциал
от обеих частей, мы получим, что
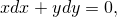
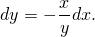 | (3) |
Первый дифференциал функции  при наложении этого условия будет
таков:
при наложении этого условия будет
таков:
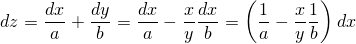
С полученным снова совершим те же действия, т.е. найдём дифференциал и учтём (3), и таким образом найдём второй дифференциал:
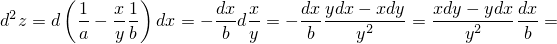
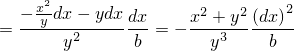
Для определения экстремумов мы должны проверить знак 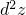 в стационарных
точках. Для всех стац. точек выполняется (2), и
в стационарных
точках. Для всех стац. точек выполняется (2), и
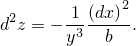
Подставим 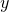 . Точка первая:
. Точка первая:
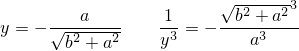
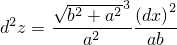
Если  и
и 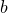 имеют один знак,
имеют один знак, 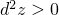 и точка
и точка 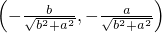 - точка
условного минимума; если разные - условного максимума.
- точка
условного минимума; если разные - условного максимума.
Точка вторая:
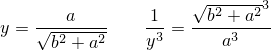
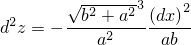
Если  и
и 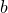 имеют один знак,
имеют один знак, 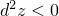 и точка
и точка 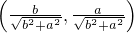 - точка
условного максимума; если разные - условного минимума.
- точка
условного максимума; если разные - условного минимума.
