Начнём с решения однородного уравнения:
Для нахождения функций
В нашем случае
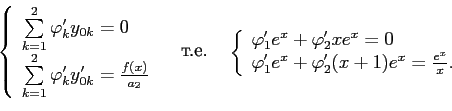
Вычтя из второго уравнения первое, получим, что
Ответ:
Начнём с решения однородного уравнения:
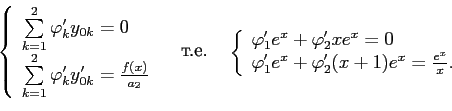
Вычтя из второго уравнения первое, получим, что
Ответ:
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников