Страница сетевой поддержки учеников Тимура Юрьевича Альпина

Найти область интегрируемости для интеграла
$$\begin{equation} \intop_{0}^{\infty}\frac{\sin x^{q}}{x^{p}}dx.\label{main} \end{equation}$$

Рассмотрим сначала вспомогательный интеграл
$$\begin{equation} \intop_{1}^{\infty}\frac{\sin x^{\alpha}}{x^{\beta}}dx\label{int_vspom} \end{equation}$$
1) $\alpha<0$. В этом случае всё подынтегральное выражение положительно, и можно применять соответствующие признаки, например, признаки сравнения. $$0<\sin x^{\alpha}\leqslant\sin1<1,\qquad\lim_{x\to\infty}\sin x^{\alpha}=0$$ $$\frac{\sin x^{\alpha}}{x^{\beta}}>0,\quad\lim_{x\to\infty}\frac{\sin x^{\alpha}}{x^{\alpha}}=1$$
Рассмотрим предел
$$\lim_{x\to\infty}\frac{\frac{\sin x^{\alpha}}{x^{\beta}}}{x^{\gamma}}=\lim_{x\to\infty}\frac{\sin x^{\alpha}}{x^{\alpha}}\frac{x^{\alpha}}{x^{\gamma+\beta}}=\lim_{x\to\infty}x^{\alpha-\gamma-\beta}$$
Этот предел существует и больше нуля только при одном значении степени:
$$\alpha-\beta-\gamma=0$$
$$\alpha-\beta=\gamma$$
Таким образом по второму признаку сравнения, интеграл функции $\frac{\sin x^{\alpha}}{x^{\beta}}$ сходится одновременно с интегралом функции $x^{\gamma}=x^{\alpha-\beta}$. Найдём область сходимости последнего:
$$\intop_{1}^{\infty}x^{\alpha-\beta}dx=\left.\frac{x^{\alpha-\beta+1}}{\alpha-\beta+1}\right|_{1}^{\infty},$$
что определено только при $\alpha-\beta+1<0$ (равенству нулю мешает знаменатель), а значит, при $\alpha<0$ интеграл $\intop_{1}^{\infty}x^{\alpha-\beta}dx$ (а значит, и интеграл ($\ref{int_vspom}$)) сходится, если $$\beta>\alpha+1.$$
2) $\alpha=0$. Тогда
$$\intop_{1}^{\infty}\frac{\sin x^{\alpha}}{x^{\beta}}dx=\sin1\intop_{1}^{\infty}x^{-\beta}dx=\left.\frac{x^{1-\beta}}{1-\beta}\right|_{1}^{\infty},$$
что определено при
$$1-\beta<0,$$ т.е. мы можем обобщить на этот случай результат предыдущего случая: $$\beta>1=\alpha+1.$$
3) $\alpha>0$. Для этого случая тоже сначала рассмотрим вспомогательный случай, результат для которого потом обобщим. Пусть сначала $\alpha=1$:
$$\intop_{1}^{\infty}\frac{\sin x^{\alpha}}{x^{\beta}}dx=\intop_{1}^{\infty}\frac{\sin x}{x^{\beta}}dx.$$
Легко видеть, что при $\beta<0$ множитель $\frac{1}{x^{\beta}}$ стремится к бесконечности, а интеграл – расходится по критерию Коши.
При $\beta=0$:
$$\intop_{1}^{\infty}\frac{\sin x}{x^{\beta}}dx=\intop_{1}^{\infty}\sin xdx=\left.\cos x\right|_{1}^{\infty}\text{ — расходится}$$

$\beta>0$: тогда $\frac{1}{x^{\beta}}$ монотонно стремится к нулю, а $\sin x$ имеет ограниченную первообразную, следовательно, интеграл
$$\intop_{1}^{\infty}\frac{\sin x}{x^{\beta}}dx$$
сходится по признаку Дирихле. В результате, при $\alpha=1$ интеграл
сходится, если $\beta>0$.

Пусть теперь $\alpha$ — произвольное положительное число. Заменим $x^{\alpha}=y$, $x=y^{1/\alpha}$, и получим
$$\intop_{1}^{\infty}\frac{\sin x^{\alpha}}{x^{\beta}}dx=\intop_{1}^{\infty}\frac{\sin y}{y^{\beta/\alpha}}\frac{1}{\alpha}y^{\frac{1}{\alpha}-1}dy=\frac{1}{\alpha}\intop_{1}^{\infty}\frac{\sin y}{y^{\frac{\beta}{\alpha}-\frac{1}{\alpha}+1}}dy,$$

а тут мы уже можем воспользоваться результатами, полученными для простого синуса в интеграле. Согласно им, для сходимости показатель степени в знаменателе должен быть положительным:
$$\frac{\beta}{\alpha}-\frac{1}{\alpha}+1>0,$$
$$\beta-1+\alpha>0,$$
$$\beta>1-\alpha.$$
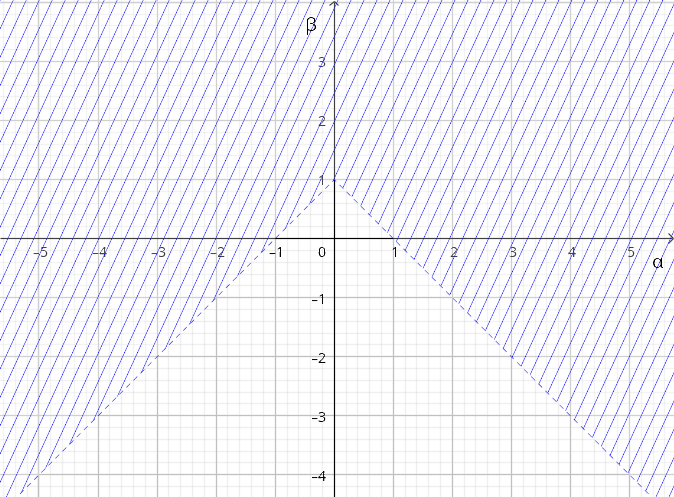
В итоге мы получаем такие условия для сходимости интеграла ($\ref{int_vspom}$): при $\alpha\leqslant0$ $\beta>1+\alpha$, а при $\alpha>0$ $\beta>1-\alpha$.

Перейдём теперь к основной задаче. Разделим область интегрирования в исходном интеграле ($\ref{main}$):
$$\begin{equation} \intop_{0}^{\infty}\frac{\sin x^{q}}{x^{p}}dx=\intop_{0}^{1}\frac{\sin x^{q}}{x^{p}}dx+\intop_{1}^{\infty}\frac{\sin x^{q}}{x^{p}}dx.\label{razb} \end{equation}$$
Второй интеграл полностью аналогичен исследованному ($\ref{int_vspom}$), и для него получаются аналогичные условия интегрируемости: при $q\leqslant0$ $p>1+q$, а при $q>0$ $p>1-q$.

В первом произведём замену $x=1/y$, $dx=-\frac{dy}{y^{2}}$:
$$\intop_{0}^{1}\frac{\sin x^{q}}{x^{p}}dx=-\intop_{\infty}^{1}\frac{\sin y^{-q}}{y^{-p}}\frac{dy}{y^{2}}=\intop_{1}^{\infty}\frac{\sin y^{-q}}{y^{2-p}}dy,$$
после чего тот тоже становится интегралом типа ($\ref{int_vspom}$). Подставляя соответствующие степени вместо $\alpha$ и $\beta$ в условия интегрируемости, получим их в таком виде: при $-q\leqslant0$ $2-p\geqslant1-q$, а при $-q>0$ $2-p>1+q$, т.е. при $q\geqslant0$ $p<1+q$, а при $q<0$ $p<1-q$ .

Интеграл ($\ref{main}$) сходится тогда, когда сходятся оба его слагаемых в разбиении ($\ref{razb}$). Следовательно, его область сходимости есть пересечение областей сходимости слагаемых: