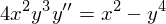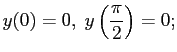диф. уравнения « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

31.05.2020

Задания и материалы для дистанционного занятия гр. 06-812 в вт 2.06.2020, 10:10 (Филиппов, №1170, 1175, 1196)

Filed under: д.у.,Дистанционное обучение,диф. уравнения,Материалы,Решения — Shine @ 11:36 пп

Образовалось одно неучтённое занятие, а так как формально у нас продолжается курс дифференциальных уравнений, хотелось бы показать ещё одну вещь, которая очень пригодится в следующем семестре на математической физике — уравнения в частных производных, хотя бы линейные и хотя бы первого порядка.

Рассмотрим линейное однородное уравнение в частных производных первого порядка в случае трёх независимых переменных: \begin{equation} Pu_{x}'+Qu_{y}'+Ru_{z}'=0,\label{or_odn} \end{equation} где $P,Q,R$ зависят от $x,y,z$.

(more…)

Comments (0)

18.11.2019

Филиппов №437 (для тов. Толмачёвой и других интересующихся)

Filed under: диф. уравнения,Решения — Shine @ 6:18 пп

Решить уравнение:
\[
y^{\prime\prime}=e^{y}
\]
(more…)

Comments (0)

19.11.2016

Интеграл из №681 для гр. 06-512

Filed under: диф. уравнения,Решения — Shine @ 4:25 пп

Студенты из гр. 512 не смогли взять интеграл, нужный для нахождения $z$. Берётся он так:
(more…)

Comments (0)

28.10.2015

Филиппов №681

Filed under: диф. уравнения,Решения — Shine @ 9:32 пп

Я задал группе 06-410 уравнения, решаемые методом Остроградского-Лиувилля, а примеров не показал. Показываю:
(more…)

Comments (0)

16.10.2013

Филиппов №794

Filed under: диф. уравнения — Shine @ 4:30 пп

Решить систему

{ ˙x = 2y− 3x, ˙y = y− 2x.

(1)

(more…)

Comments (0)

14.10.2013

Давно обещал

Filed under: диф. уравнения — Shine @ 1:20 пп

Тов. Ларин интересовался, как решается первое уравнение из третьего варианта

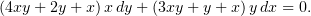
(4xy+ 2y+ x) xdy+ (3xy+ y + x)ydx = 0.

Решается оно так.

(more…)

Comments (0)

03.10.2012

Метод вариации постоянных и разное

Filed under: диф. уравнения,пепел — Shine @ 3:22 пп

Что-то занесло меня сегодня.
Во-первых: в №551 коэффициенты неоднородного решения такие:
a=-5/8,~b=0,~c=0, d=5/16 .
Во-вторых, в конце занятия я пытался, но не смог объяснить следующее:
(more…)

Comments (0)

01.12.2011

Бесплатные советы по решению лин. неодн. диф. уравнений

Filed under: диф. уравнения — Shine @ 9:41 пп

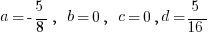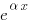Перед тем, как решать линейное неоднородное уравнение, можно сделать вот что. Если в его правой части есть множитель вида $e^{alpha x}$ , можно заменить искомую функцию по формуле 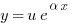$y=u e^{alpha x}$ . После замены множитель $e^{alpha x}$ сократится во всём уравнении, причём линейность не испортится и порядок не повысится.
Однако счёт после такой подстановки может ускориться в разы, особенно для уравнений высоких порядков. Связано это с тем, что частное решение при каждом диффренцировании сильно разрастается по количеству слагаемых, и сокращение $e^{alpha x}$ позволяет уменьшить это разрастание.
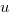После нахождения общего решения уравнения на оно подставляется в формулу замены, по которой находится .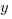