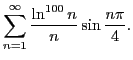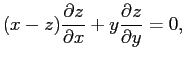Правильный вариант решения, которое я писал на доске для гр. 661. В аудитории
я где-то ошибся, теперь трудно сказать где.
(more…)
11.02.2017
Демидович, № 2242
08.05.2016
26.04.2015
Демидович, № 2424.3 (площадь в полярных координатах)
В новой нумерации, вероятно, эта задача называется 2424 в)
Найти площадь фигуры, ограниченной линиями:
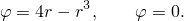
19.04.2015
02.04.2015
29.03.2015
Пояснения для гр. 06-403 по методу Лагранжа
20.02.2015
Площадь сектора
Я не успел вывести формулу для площади криволинейного сектора. Выкладываю этот вывод, заодно напомню его начало в более понятном виде. Кто хорошо понял начало вывода - те могут начинать читать с формулы (1).
03.03.2013
Группе 621
Простите меня, в субботу я наговорил ерунды.
При применении второго метода второй дифференциал при наличии связи мы считали так:
- функцию дифференцировали два раза,
- В полученный второй дифференциал подставляли приращения некоторых свободных переменных, полученные из уравнения связи.
А он вычисляется сложнее:
- Функция дифференцируется однажды;
- В первый дифференциал подставляются приращения (до этого места дело уже сделано при исследовании необходимых условий, т.е. когда искались точки возможного экстремума);
- Первый дифференциал дифференцируется ещё раз;
- Опять подставляются приращения.
Этот алгоритм в нормере №3655 (который мы кое-как, каменными топорами, добили) выглядит так.
за функцию, а 
и 
- за независимые переменные.
