Запутали вы меня, тов. Ханафиева и тов. Мубаракшин. Впрочем, я сам хорош, если вам это удалось.
08.11.2013
30.10.2013
к гр. 625
Сегодня решение уравнения 681 свелось к уравнению
.
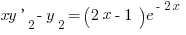Решение искалось в виде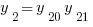 
. Мы быстро нашли, что 
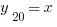, а 
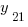был найден в виде интеграла: 
.
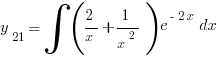Этого интеграла я испугался. Ноутбук тоже. А интеграл, меж тем, легко берётся, если заметить, что:
,
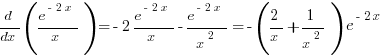и тогда
.
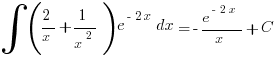При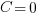 
имеем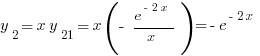 
. Вспомнив, что 
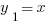, запишем общее решение уравнения 681:
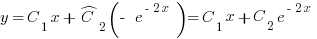, где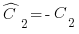 
,
что и написано в ответе из задачника.
Возникает вопрос, как можно угадать такую первообразную. Чтобы её не приходилось угадывать, из правой части уравнения можно убрать множитель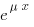 
, воспользовавшись методом, изложеным здесь.
03.03.2013
Группе 621
Простите меня, в субботу я наговорил ерунды.
При применении второго метода второй дифференциал при наличии связи мы считали так:
- функцию дифференцировали два раза,
- В полученный второй дифференциал подставляли приращения некоторых свободных переменных, полученные из уравнения связи.
А он вычисляется сложнее:
- Функция дифференцируется однажды;
- В первый дифференциал подставляются приращения (до этого места дело уже сделано при исследовании необходимых условий, т.е. когда искались точки возможного экстремума);
- Первый дифференциал дифференцируется ещё раз;
- Опять подставляются приращения.
Этот алгоритм в нормере №3655 (который мы кое-как, каменными топорами, добили) выглядит так.
03.10.2012
Метод вариации постоянных и разное
Что-то занесло меня сегодня.
Во-первых: в №551 коэффициенты неоднородного решения такие:
.
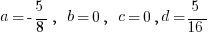Во-вторых, в конце занятия я пытался, но не смог объяснить следующее:
(more…)
23.03.2011
Гр. 697,
я вас запутал лишнего. Когда в задаче 4.24 мы рассмотрели функцию $w=\frac{1}{z}$, переводящую смещённую вверх единичную окружность $x^2+(y-1)^2=1$ в смещённую вниз прямую $v=-\frac{1}{2}$, надо было по ней построить функцию, переводящую единичную окружность с центром в нуле в ось действительных чисел: $w=\frac{1}{z+i}+\frac{i}{2}$. И уже эту функцию надо было обращать. При этом мы получили бы функцию $w=-\frac{2iz-1}{2z-i}$, переводящую верхнюю полуплоскость в единичный круг.
06.09.2010
Наврал-с
Наврал я группе №687. Конечно же,
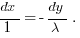
Через отсутствие этого минуса и весь грех произошёл.
30.03.2010
Нагородил
Простите, гр.682, я нагнал вам лютой пурги. Вот как должно было выглядеть объяснение формулы Коши и примера 5.15:
