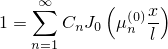Итак, мы искали
\[
U\left(t,r,\varphi\right)=T\left(t\right)R\left(r\right)\Phi\left(\varphi\right)H\left(h\right),
\]
и получили, что
(more…)
08.12.2021
О преодолении одного принципиального затруднения в №122 из Даишева и Никитина
21.10.2021
Даишев, Никитин №78
Помимо того, что в ответе многого не хватало, неясно, почему там не взяли второй интеграл — а он тоже Эйлера-Пуассона. Ответ получается вполне компактный.
Решение содержит много копипасты из решения №77, так что смотреть можно с середины.
25.11.2020
Задания и материалы для дистанционного занятия гр. 06-812 в 14:00 в ср. 25.11.2020 (Даишев, Никитин № 100)
Задание: Для разминки решите №96 и 97. Они столь просты, что не требуют пояснений.
18.11.2020
Задания и материалы для дистанционного занятия гр. 06-812 в 14:00 в ср. 18.11.2020 (Даишев, Никитин № 93 а), 83, 85)
Уравнению Бесселя \[ y''+\frac{1}{x}y'+\left(1-\frac{\nu^{2}}{x^{2}}\right)y=0 \] удовлетворяют функции Бесселя: \[ J_{\pm\nu}\left(x\right)=\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}}{\Gamma\left(k\pm\nu+1\right)k!}\left(\frac{x}{2}\right)^{2k\pm\nu}. \]
30.10.2015
28.09.2015
Даишев, Никитин №26
Эту задачу на занятии с гр. №304 мы начали делать, считая на границах саму искомую функцию равной нулю. Занятие это было тоже небесполезно, но в самой задаче граничные условия были другими: справа занулялась производная. Задачи с разными граничными условиями встречаются, однако, нередко, так что желательно знать, как они решаются. Итак:
Найти решение уравнения:
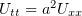 | (1) |
Граничные условия:
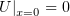 | (2) |
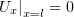 | (3) |
Начальные условия:
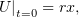 | (4) |
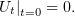 | (5) |
17.04.2015
Даишев, Никитин №100
19.12.2014
O RLY?
Стало модно писать, что интеграл от чётной функции по симметричному относительно нуля промежутку равен нулю.
Сомневаюсь.
Ну хотя бы:
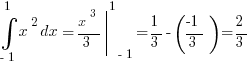
26.11.2014
В задаче №102 из Даишева и Никитина сказано разложить по функциям второго порядка, но ответ дан с функциями нулевого. Попробуйте разложить так, если это не поможет — обращайтесь ещё раз.
17.10.2014
Даишев, Никитин №53
Решение этого номера, запрошенное многими, не выкладывается в связи с тем, что оно годно изложено в методичке.
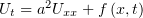
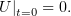
![x ∈ [0,l]](http://shine.ylsoftware.com/math-img/dn100/dn1000x.png) , т.е. представить её в виде
, т.е. представить её в виде