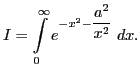Сентябрь « 2011 « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

29.09.2011

Демидович, №3807

Filed under: мат. ан. сем. 3 — Shine @ 8:20 пп

Найти величину интеграла:

$\displaystyle I=\int\limits_{0}^{\infty }{e^{-x^2-\dfrac{a^2}{x^2}}\;dx}.$

(1)

(more…)

Comments (0)

Задание на дом по д/у для гр.606

Filed under: Домашнее задание — Shine @ 8:04 пп

Демидович, 3853-3859.

Comments (0)

21.09.2011

Filed under: Домашнее задание — Shine @ 12:35 дп

Задание для группы 606 по мат. анализу на четверг:
Демидович, 3813-3816
Обращаю ваше особое внимание на то, что в 3814 и 3815 нельзя дифференцировать по параметрам исходные интегралы — производные не будут сходиться.

Comments (0)

16.09.2011

Filed under: Домашнее задание — Shine @ 8:53 дп

Задание для группы 606 по мат. анализу (занятие будет во вторник):
Демидович, 3795, 3796, 3798, 3799, 3804, 3806.

Comments (0)

13.09.2011

Даишев, Никитин №7

Filed under: ММФ — Shine @ 2:41 пп

Группа 692, в сабже при замене
delim{lbrace}{ matrix{2}{2}{ {s=} {y-cos(x)-x} {t=} {y-cos(x)+x} } }{}
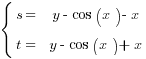
уравнение упрощается до формы 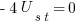$-4U_{s t}=0$ , если у вас получается что-то ещё — ищите ошибки.

Comments (0)

11.09.2011

Демидович, № 3726

Filed under: мат. ан. сем. 3 — Shine @ 9:56 пп

Доказать, что функция Бесселя \[ J_{n}\left(x\right)=\frac{1}{\pi}\intop_{0}^{\pi}\cos\left(n\varphi-x\sin\varphi\right)d\varphi,\quad n\in\mathbb{Z} \] удовлетворяет уравнению Бесселя \[ x^{2}J_{n}''\left(x\right)+xJ_{n}'\left(x\right)+\left(x^{2}-n^{2}\right)J_{n}\left(x\right)=0. \]

(more…)

Comments (0)

09.09.2011

гр.603,

Filed under: кто что где когда — Shine @ 10:33 дп

По понедельникам начиная с 12.09 начнётся ММФ.
Сначала мне на этот час поставили мат.анализ, потом втихаря изменили расписание, поэтому вы не дождались меня в этот понедельник.
Так как в ауд. 1201 нет розетки, я обменял её на ауд 806, так что приходите туда.

Comments (0)

Задание на дом по д/у для гр.606

Filed under: Домашнее задание — Shine @ 10:30 дп

Номера из Филиппова: 108-111, 117, 119, 120, 123-125, 142-144, 147, 150

Comments (0)