Найти суммы рядов
Я покажу, как это сделать без комплексных чисел.
Я задал группе 06-410 уравнения, решаемые методом Остроградского-Лиувилля, а примеров не показал. Показываю:
(more…)
Эту задачу на занятии с гр. №304 мы начали делать, считая на границах саму искомую функцию равной нулю. Занятие это было тоже небесполезно, но в самой задаче граничные условия были другими: справа занулялась производная. Задачи с разными граничными условиями встречаются, однако, нередко, так что желательно знать, как они решаются. Итак:
Найти решение уравнения:
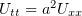 | (1) |
Граничные условия:
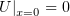 | (2) |
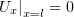 | (3) |
Начальные условия:
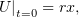 | (4) |
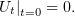 | (5) |
Тов. Фаляхова, я неправильно проверил Вашу последнюю контрольную работу. Баллы после исправления: 5/0/4.
В новой нумерации, вероятно, эта задача называется 2424 в)
Найти площадь фигуры, ограниченной линиями:
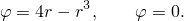
Хостингом угостил Вадим "Moose" Калинников