Решить систему
 | (1) |
16.10.2013
14.10.2013
Давно обещал
Тов. Ларин интересовался, как решается первое уравнение из третьего варианта
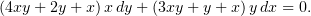
Решается оно так.
12.10.2013
Восстановление дифференцируемой функции
Ещё одно пояснение для гр. 620а.
Условия Коши-Римана позволяют восстановить дифференцируемую функцию
по её действительной или мнимой части, если известно её значение в какой-либо
точке. Например, решить такую задачу:
(more…)
Другой вид условий Коши-Римана
.
Действительные числа, фиксирующие комплексное число при этих двух
способах его задания, связаны так:
03.03.2013
Группе 621
Простите меня, в субботу я наговорил ерунды.
При применении второго метода второй дифференциал при наличии связи мы считали так:
- функцию дифференцировали два раза,
- В полученный второй дифференциал подставляли приращения некоторых свободных переменных, полученные из уравнения связи.
А он вычисляется сложнее:
- Функция дифференцируется однажды;
- В первый дифференциал подставляются приращения (до этого места дело уже сделано при исследовании необходимых условий, т.е. когда искались точки возможного экстремума);
- Первый дифференциал дифференцируется ещё раз;
- Опять подставляются приращения.
Этот алгоритм в нормере №3655 (который мы кое-как, каменными топорами, добили) выглядит так.
28.02.2013
06.12.2012
31.10.2012
1. В тригонометрии вводились (и даже доказывались) такие формулы:
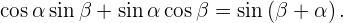
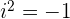, вычислим:
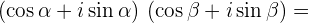
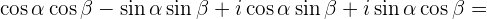 | (1) |
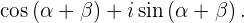
2. Теперь пусть в формуле (1)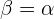 
:
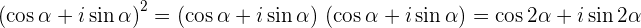
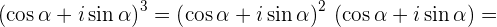
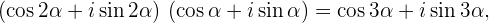
03.10.2012
Метод вариации постоянных и разное
Что-то занесло меня сегодня.
Во-первых: в №551 коэффициенты неоднородного решения такие:
.
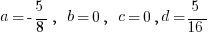Во-вторых, в конце занятия я пытался, но не смог объяснить следующее:
(more…)
