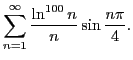
я вас запутал лишнего. Когда в задаче 4.24 мы рассмотрели функцию $w=\frac{1}{z}$, переводящую смещённую вверх единичную окружность $x^2+(y-1)^2=1$ в смещённую вниз прямую $v=-\frac{1}{2}$, надо было по ней построить функцию, переводящую единичную окружность с центром в нуле в ось действительных чисел: $w=\frac{1}{z+i}+\frac{i}{2}$. И уже эту функцию надо было обращать. При этом мы получили бы функцию $w=-\frac{2iz-1}{2z-i}$, переводящую верхнюю полуплоскость в единичный круг.
Наврал я группе №687. Конечно же,
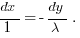
Через отсутствие этого минуса и весь грех произошёл.
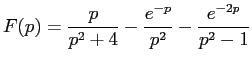
Хостингом угостил Вадим "Moose" Калинников