Просили выложить решения к номерам 11, 12 и 13. Они решаются общим
методом: заменяется искомая функция по формуле 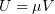 , где
, где 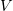 будет
новой искомой функцией, а
будет
новой искомой функцией, а 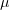 ищется из соображений максимального удобства.
Мы будем подбирать
ищется из соображений максимального удобства.
Мы будем подбирать 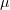 так, чтобы функция
так, чтобы функция 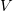 входила в уравнение только в
виде вторых производных.
входила в уравнение только в
виде вторых производных.
20.09.2014
Даишев, Никитин №№ 11, 12, 13
16.09.2014
Раздаточный материал
PDF с решением № 25 из Даишева и Никитина.
Для тех, кто набредёт на этот файл случайно: это формульная часть, и она нуждается в словесных пояснениях.
12.09.2014
06.09.2014
Некоторые пояснения по каноническому виду уравнений 2-го порядка (ММФ)
ОБН 11.09.2014 поправил ересь в конце.
Про эллиптические уравнения всем группам, кроме 06-206, я не привёл никаких обоснований, а группе 06-206 наговорил общих слов. Вероятно, вам всё ещё интересно, почему описанные мной действия с ними дают неизменно превосходный результат.
13.10.2011
13.09.2011
Даишев, Никитин №7
Группа 692, в сабже при замене
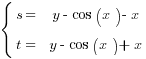
уравнение упрощается до формы 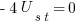 , если у вас получается что-то ещё — ищите ошибки.
, если у вас получается что-то ещё — ищите ошибки.
21.12.2009
Даишев, Никитин №127
Циллиндр с радиусом основания 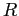 и высотою
и высотою 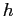 имеет во всё время опыта температуру нижнего основания и боковой поверхности, равную 0
, а температура верхнего основания есть определённая функция от
имеет во всё время опыта температуру нижнего основания и боковой поверхности, равную 0
, а температура верхнего основания есть определённая функция от 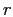 . Найти стационарную температуру внутренних точек циллиндра.
. Найти стационарную температуру внутренних точек циллиндра.

