Найти предел
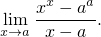
В качестве компенсации за сорванное сегодня занятие могу объяснить одно старое домашнее задание.
Номер 66. Доказать, что
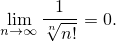
Ничем особенным решение систем от решения одинарных уравнений не отличается. Но, раз обещал выложить — выкладываю.
Решить систему
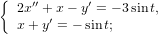
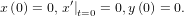
Перед тем, как решать линейное неоднородное уравнение, можно сделать вот что. Если в его правой части есть множитель вида 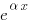 , можно заменить искомую функцию по формуле
, можно заменить искомую функцию по формуле 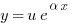 . После замены множитель
. После замены множитель 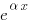 сократится во всём уравнении, причём линейность не испортится и порядок не повысится.
сократится во всём уравнении, причём линейность не испортится и порядок не повысится.
Однако счёт после такой подстановки может ускориться в разы, особенно для уравнений высоких порядков. Связано это с тем, что частное решение при каждом диффренцировании сильно разрастается по количеству слагаемых, и сокращение 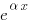 позволяет уменьшить это разрастание.
позволяет уменьшить это разрастание.
После нахождения общего решения уравнения на 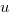 оно подставляется в формулу замены, по которой находится
оно подставляется в формулу замены, по которой находится 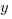 .
.
Вычислить поверхностный интеграл второго рода
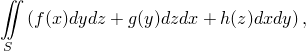
где 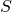 – внешняя сторона поверхности параллелепипеда
– внешняя сторона поверхности параллелепипеда  ;
; 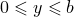 ;
;
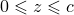 .
.
Хостингом угостил Вадим "Moose" Калинников