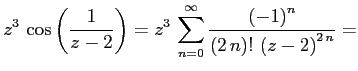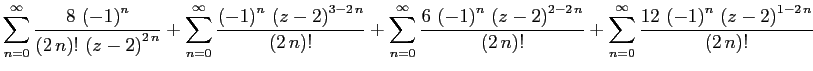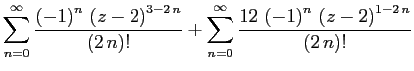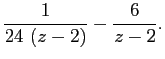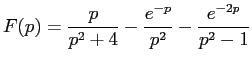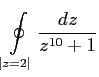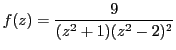Вывод для гр. 620а, который я не успел сделать на занятии.
Как известно, комплексное число можно представить как в алгебраической, так и в
тригонометрической/показательной формах: 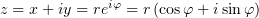 .
Действительные числа, фиксирующие комплексное число при этих двух
способах его задания, связаны так:
.
Действительные числа, фиксирующие комплексное число при этих двух
способах его задания, связаны так:
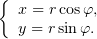 | (1) |
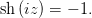
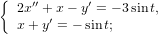
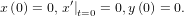
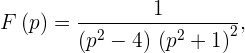
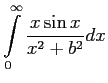
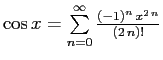 , представим функцию
, представим функцию