Найти экстремумы функции
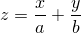 | (1) |
при условии
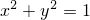 | (2) |
Я не успел вывести формулу для площади криволинейного сектора. Выкладываю этот вывод, заодно напомню его начало в более понятном виде. Кто хорошо понял начало вывода - те могут начинать читать с формулы (1).
Стало модно писать, что интеграл от чётной функции по симметричному относительно нуля промежутку равен нулю.
Сомневаюсь.
Ну хотя бы:
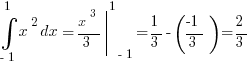
В задаче №102 из Даишева и Никитина сказано разложить по функциям второго порядка, но ответ дан с функциями нулевого. Попробуйте разложить так, если это не поможет — обращайтесь ещё раз.
Решение этого номера, запрошенное многими, не выкладывается в связи с тем, что оно годно изложено в методичке.
Файл с решением задачи №52 обновлён, поправлены мелкие ошибки.
Просьба к заинтересованным людям перекачать его заново.
Просили выложить решения к номерам 11, 12 и 13. Они решаются общим
методом: заменяется искомая функция по формуле 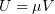 , где
, где 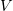 будет
новой искомой функцией, а
будет
новой искомой функцией, а 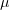 ищется из соображений максимального удобства.
Мы будем подбирать
ищется из соображений максимального удобства.
Мы будем подбирать 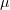 так, чтобы функция
так, чтобы функция 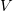 входила в уравнение только в
виде вторых производных.
входила в уравнение только в
виде вторых производных.
PDF с решением № 25 из Даишева и Никитина.
Для тех, кто набредёт на этот файл случайно: это формульная часть, и она нуждается в словесных пояснениях.
Хостингом угостил Вадим "Moose" Калинников