Страница сетевой поддержки учеников Тимура Юрьевича Альпина

В уравнении \[ z_{xx}''+z_{yy}''+m^{2}z=0 \] произвести замену \[ \left\{ \begin{array}{c} x=e^{u}\cos v,\\ y=e^{u}\sin v. \end{array}\right. \]

(more…)

Найдём $d^{10}u$ от \[ u=\ln\left(x+y\right). \]

(more…)

Почему-то вызвал трудности №2439. В нём надо было найти длину кривой, заданной уравнением \[ y^{2}=\frac{x^{3}}{2a-x}. \] (more...)

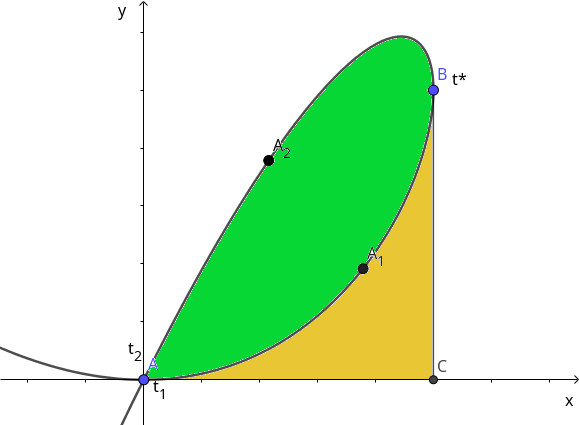
Задача на объём — в помощь тем, кто разбирается с телами вращения.

Найти объём тела, полученного при вращении кривой \begin{equation} x^{2}-xy+y^{2}=a^{2}\label{main} \end{equation} вокруг оси $Ox$.

(more...)

Решение, которое я не успел показать, привожу тут. Разобьём исходный интеграл по двум половинам исходного промежутка интегрирования:
\[
\intop_{0}^{2\pi}\frac{dx}{1+\varepsilon\cos x}=\intop_{0}^{\pi}\frac{dx}{1+\varepsilon\cos x}+\intop_{\pi}^{2\pi}\frac{dx}{1+\varepsilon\cos x}=
\]
(more…)

Задача у народа плохо пошла, поэтому выкладываю. Площадь сечения найдена без интегралов, из соображений школьной геометрии.

Найти объём, ограниченный поверхностями
\[
x^{2}+y^{2}+z^{2}=a^{2},\qquad x^{2}+y^{2}=ax.
\]
(more…)