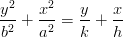Найти область интегрируемости для интеграла
\begin{equation}
\intop_{0}^{\infty}\frac{\sin x^{q}}{x^{p}}dx.\label{main}
\end{equation}
(more…)
13.10.2019
Демидович, № 3743
09.10.2019
Ещё раз к вопросу о равномерной сходимости интеграла в №3784
Для обоснования возможности хотя бы дифференцирования по $n$ интеграла
\[
\intop_{0}^{1}x^{n-1}dx=\frac{1}{n}
\]
(more…)
01.12.2017
Ещё раз к вопросу о параметризации в №4238
Я вчера неправильно описал интересовавшимся товарищам повёрнутый эллипс в общем случае.
07.12.2016
Демидович, №4013
Переходя к полярным координатам, найти объемы тел, ограниченных следующими
поверхностями:
\[
z^{2}=xy,\quad x^{2}+y^{2}=a^{2}.
\]
15.11.2016
Альтернативное решение задачи 3988
Я уже выкладывал решение этой задачи тут, и будет полезно сначала
прочитать то решение – тут процесс описывается с середины.
В старом решении площадь была сведена к интегралу с шестыми степенями в знаменателе,
а его взятие, невоспроизводимое за разумное время, было совершенно опущено. В этой заметке описывается решение
этой задачи без трудовых подвигов.
25.09.2015
Демидович, №2361
09.11.2011
Демидович №4363
Вычислить поверхностный интеграл второго рода
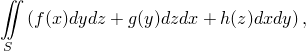
где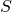 
– внешняя сторона поверхности параллелепипеда 
; 
;
.
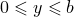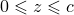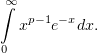
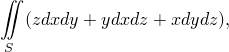
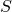– внешняя сторона сферы 
.
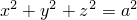– поверхность
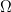, ограниченной графиком уравнения:
