Найти область сходимости интеграла \begin{equation} \int\limits _{0}^{\infty}\frac{x^{p-1}\ln x}{1+x}dx.\label{int} \end{equation} Я понял: надо было брать мажорирующую функцию прямо вместе с логарифмом.
15.10.2021
07.12.2020
Задания и материалы для дистанционного занятия гр. 06-912 в 8:30 в пн. 7.12.2020 (Демидович № 4224, 4252)
Здравствуйте. Материал для освоения вот, я на связи жду вопросов. Д/з в честь прошедшей к/р не проверяется.
23.11.2020
Демидович № 4022
Найти объём тела, ограниченного поверхностями ($a,b,c > 0$): \[ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=-1,\qquad\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1. \]
Демидович № 4009
Найти объём тела, ограниченного поверхностями: \[ z=x^{2}+y^{2},\quad y=x^{2},\quad y=1,\quad z=0. \]
19.11.2020
Задания и материалы для дистанционного занятия гр. 06-912 в 10:10 в чт. 19.11.2020 (Демидович № 4103, 4108)
Объём тела равен интегралу от единицы по этому телу: \[ V=\iiint\limits_{V}1\cdot dxdydz \]
17.11.2020
Демидович № 3992
Вводя обобщённые полярные координаты, найти площадь, ограниченную кривыми: \[ \frac{x^{3}}{a^{3}}+\frac{y^{3}}{b^{3}}=\frac{x^{2}}{h^{2}}+\frac{y^{2}}{k^{2}},\qquad x=0,\quad y=0. \]
28.10.2020
Демидович № 3962
Произведя соответствующую замену переменных, свести двойной интеграл \[ \iint\limits _{\left|x\right|+\left|y\right|\leqslant1}f\left(x+y\right)dxdy \] к однократному.
Демидович № 3957
В интеграле \[ \int\limits _{a}^{b}dx\int\limits _{\alpha x}^{\beta x}dyf\left(x,y\right),\qquad0 < a < b,\quad0 < \alpha < \beta, \] перейти к переменным: $u=x$, $v=y/x$ (обратно можно выразить $x=u$, $y=vx=uv$).
Демидович № 3953
Переходя к полярным координатам, заменить двойной интеграл \[ \iint\limits _{x^{2}+y^{2}\leqslant x}f\left(\frac{y}{x}\right)dxdy \] однократным.
27.10.2020
Демидович № 3944
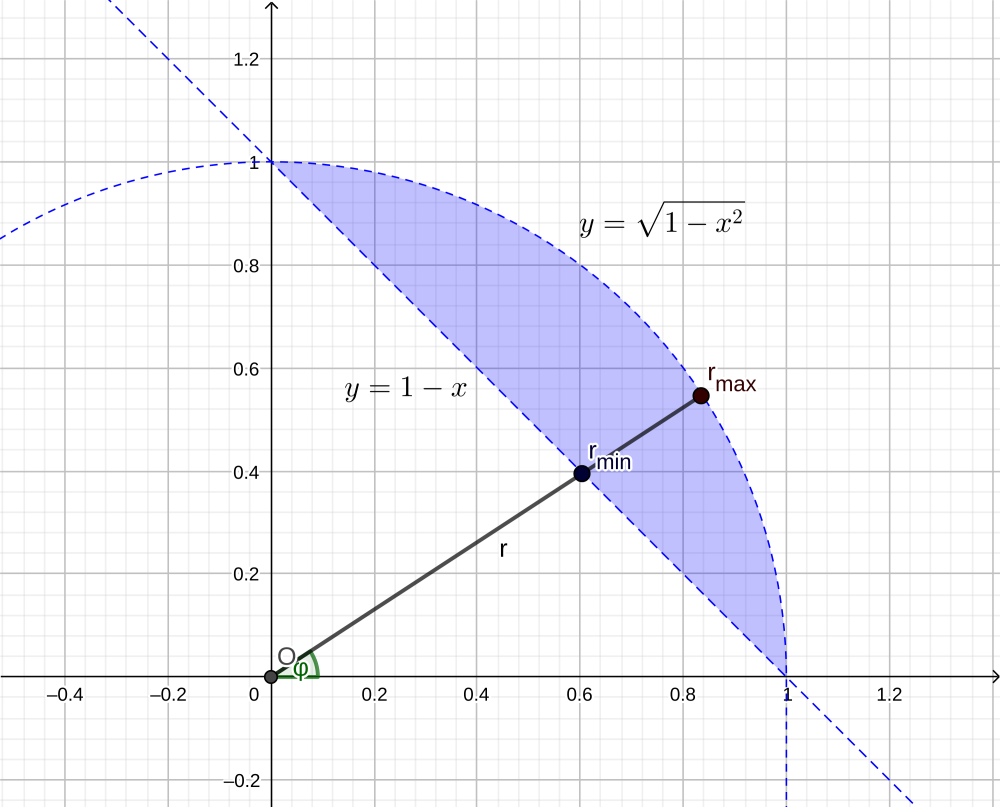
Перейти к полярным координатам и расставить пределы интегрирования в том и в другом порядке в интеграле:
\[
\intop_{0}^{1}dx\intop_{1-x}^{\sqrt{1-x^{2}}}dyf\left(x,y\right)
\]