Решения « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

12.09.2014

Даишев, Никитин №№ 8 и 9

Filed under: ММФ,Решения — Shine @ 2:43 дп

Уравнение №8:

x2Uxx − 2xyUxy +y2Uyy + xUx + yUy = 0.

(more…)

Comments (0)

06.09.2014

Некоторые пояснения по каноническому виду уравнений 2-го порядка (ММФ)

Filed under: ММФ,Решения — Shine @ 1:15 дп

ОБН 11.09.2014 поправил ересь в конце.

Про эллиптические уравнения всем группам, кроме 06-206, я не привёл никаких обоснований, а группе 06-206 наговорил общих слов. Вероятно, вам всё ещё интересно, почему описанные мной действия с ними дают неизменно превосходный результат.

(more…)

Comments (0)

03.04.2014

Анчиков №138

Filed under: век. ан.,Решения — Shine @ 11:25 пп

Найти веторный потенциал поля $⃗F = 2y⃗i− z⃗j + 2x⃗k$ .

(more…)

Comments (0)

23.12.2013

Filed under: пепел — Shine @ 5:50 пп

Уважаемый тов. Зиннатуллин (гр. 6211)!
Я перепроверил Ваши контрольные работы более тщательно и оценил решение их задач на 5-3 и 3-2 соответственно. При желании Вы можете подойти и узнать подробное обоснование этих оценок. Итого за семестр Вы набираете 32 балла.
Приношу извинения за проявленную ранее невнимательность.

Comments (0)

20.12.2013

Filed under: кто что где когда,пепел — Shine @ 2:47 пп

Завтра у гр. 6210, как я и обещал (но забыл), будет к/р по кратным интегралам (преимущественно двойным) и их применениям (объёмы, площади).
Приношу извинения за введение в заблуждение.

Comments (0)

11.12.2013

Решение однородного уравнения Фредгольма второго рода

Filed under: ВИиИУ,Решения — Shine @ 6:50 пп

Найти ненулевые решения уравнения (этого уравнения нет в задачнике):

∫π y (x) = λ y (t)sin (x− t)dt. 0

(1)

(more…)

Comments (0)

Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром, не требующее забитой формулами головы

Filed under: ВИиИУ,Решения — Shine @ 5:16 пп

Решить уравнение:

∫1 y(x) = 2 (sin2π(x − t)− 2)y (t)dt+ 5x. 0

(more…)

Comments (0)

26.11.2013

Из домашнего задания гр.620а (по просьбе тов. Улахович)

Filed under: ТФКП — Shine @ 7:31 пп

Восстановить аналитическую функцию 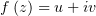$f (z) = u+ iv$ , про которую известно, что она:

1) Имеет мнимую часть 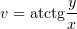$v = atctg y x$ ,

2) Имеет известное значение в некоторой точке: 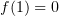$f(1) = 0$ .

(more…)

Comments (0)

08.11.2013

Ти ж мене пiдманула

Filed under: пепел,ТФКП — Shine @ 2:18 пп

Запутали вы меня, тов. Ханафиева и тов. Мубаракшин. Впрочем, я сам хорош, если вам это удалось.

(more…)

Comments (0)

30.10.2013

к гр. 625

Filed under: пепел — Shine @ 3:09 пп

Сегодня решение уравнения 681 свелось к уравнению
$xy^,_2-y_2=(2x-1)e^{-2x}$ .
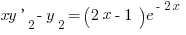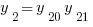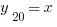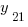Решение искалось в виде $y_2=y_{20}y_{21}$ . Мы быстро нашли, что $y_{20}=x$ , а $y_{21}$ был найден в виде интеграла: $y_{21}=int{}{}{(2/x+1/x^2)e^{-2x} dx}$ .

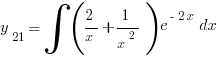Этого интеграла я испугался. Ноутбук тоже. А интеграл, меж тем, легко берётся, если заметить, что:
$d/dx (e^{-2x}/x)=-2 e^{-2x}/x - e^{-2x}/x^2 = -(2/x + 1/x^2)e^{-2x}$ ,
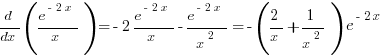и тогда
$int{}{}{(2/x+1/x^2)e^{-2x} dx}=- e^{-2x}/x +C$ .
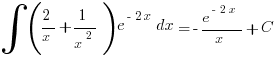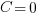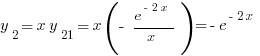При C=0 имеем $y_2=x y_{21}=x (- e^{-2x}/x)=- e^{-2x}$ . Вспомнив, что 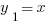$y_{1}=x$ , запишем общее решение уравнения 681:
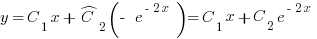$y=C_1 x + hat{C}_2 (- e^{-2x})=C_1 x + C_2 e^{-2x}$ , где $hat{C}_2=-C_2$ ,
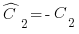что и написано в ответе из задачника.

Возникает вопрос, как можно угадать такую первообразную. Чтобы её не приходилось угадывать, из правой части уравнения можно убрать множитель 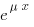$e^{mu x}$ , воспользовавшись методом, изложеным здесь.

Comments (0)

« Newer Posts — Older Posts »